A comparison study between three different Kernel estimators for the Hazard rate function
Abstract
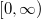 , its will be under the boundary effect near zero when the estimation is done using symmetric kernels such as the Gaussian kernel. Two kernel estimators for the hazard rate function were proposed using asymmetric kernels are the Reciprocal Inverse Gaussian and Inverse Gaussian kernel estimators to avoid the high bias near zero. In this paper, we propose a theoretical comparison between those estimators by looking at their asymptotic bias, variance and the mean squared error. Also, a comparison of the practical performance of the two estimators based on simulated and real data will be present.
, its will be under the boundary effect near zero when the estimation is done using symmetric kernels such as the Gaussian kernel. Two kernel estimators for the hazard rate function were proposed using asymmetric kernels are the Reciprocal Inverse Gaussian and Inverse Gaussian kernel estimators to avoid the high bias near zero. In this paper, we propose a theoretical comparison between those estimators by looking at their asymptotic bias, variance and the mean squared error. Also, a comparison of the practical performance of the two estimators based on simulated and real data will be present.References
Cox, D.: Oakes, D.: Analysis of survival data, Chapman and Hall, (1984).
Chen, S.X.: Probability density function estimation using gamma kernels, Ann. Inst.
Stat. Math,52,471-480,(2000).
Loprinzi, C.L.: Laurie, J.A.: Et al.,.: Prospective evaluation of prognostic vari-
ables from patient-completed questionnaires, Journal of Clinical Oncology, 12(3):601-
, (1994).
Salha, R.: Estimating the Density and Hazard Rate Functions Using Reciprocal
Inverse Gaussian Kernel, ASMDA conference, Barcelona, 25-28, (2013).
Salha, R.: Hazard rate function estimation using inverse Gaussian kernel, The
Islamic university of Gaza journal of Natural and Engineering studies,20(1), 73-
,(2012).
Salha, R.: Adaptive kernel estimation of the hazard rate function, The Islamic
university of Gaza Journal of Natural and Engineering studies, 17(1), 71-81, (2009).
Scaillet, O.: Density estimation using inverse and reciprocal inverse Gaussian
kernels, Nonparametric Statistics, 16, 217-226, (2004).
Silverman, B.: Density Estimation for Statistics and Data analysis, Chapman and
Hall, (1986).
Watson, G.: Leadbetter, M.: Hazard analysis I, Biometrika, 51, 175-184, (1995).
Full Text: pdf


