More on the Generalized fuzzy entropy of order 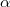 and
and 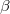
Abstract
Generalized fuzzy entropy is more comprehensive than standard fuzzy entropy, as it enhances the performance in theory and application.
New generalized fuzzy entropies are proposed and analyzed. The two proposed measures satisfied the axiomatic requirements of De Luca and Termini(1972).
Real life example is studied and the performance of the new measuresis noted and compared to other measures. and hence the validation of the measures is established.
References
Al-Talib, M. and Al-Nasser, A. (2018). New fuzzy entropy measure of order . Pakistan Journal of Statistics and Operation Research, pages 831{838.
Amigo, J. M., Balogh, S. G., and Hernandez, S. (2018). A brief review of generalized entropies. Entropy, 20(11):813.
Bhandari, D. and Pal, N. R. (1993). Some new information measures for fuzzy sets. Information Sciences, 67(3):209{228.
Cover, T. M. and Thomas, J. A. (2006). Elements of information theory 2nd edition (wiley series in telecommunications and signal processing).
De Luca, A. and Termini, S. (1972). A denition of a nonprobabilistic entropy in the setting of fuzzy sets theory. Information and control, 20(4):301{312.
Furuichi, S., Minculete, N., and Mitroi, F.-C. (2012). Some inequalities on generalized entropies. Journal of Inequalities and Applications, 2012(1):1{16.
Hung, W.-L. and Yang, M.-S. (2006). Fuzzy entropy on intuitionistic fuzzy sets. International Journal of Intelligent Systems, 21(4):443{451.
Joshi, R. and Kumar, S. (2018). An (r, s)-norm fuzzy information measure with its applications in multiple-attribute decision-making. Computational and Applied Mathematics, 37(3):2943{2964.
Kumar, V. and Singh, N. (2018). Quantile-based generalized entropy of order (, ) for order statistics. Statistica, 78(4):299{318. Electronic Journal of Applied Statistical Analysis 9
Renyi, A. (1961). On measures of entropy and information. In Proceedings of the Fourth Berkeley Symposium on Mathematical Statistics and Probability, Volume 1: Contributions to the Theory of Statistics, pages 547{561. University of California Press.
Shannon, C. E. (1948). A mathematical theory of communication. The Bell system technical journal, 27(3):379{423.
Tsallis, C. (1988). Possible generalization of boltzmann-gibbs statistics. Journal of statistical physics, 52(1):479{487.
Varma, R. (1966). Generalizations of renyis entropy of order . Journal of Mathematical Sciences, 1(7):34{48.
Zadeh, L. A. (1965). Fuzzy sets. Information and Control, (8):338{353.
Zadeh, L. A. (1968). Probability measures of fuzzy events. Journal of mathematical analysis and applications, 23(2):421{427.
Full Text: pdf


