Generalizations of the Inverse Weibull and Related Distributions with Applications
Abstract
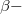 entropy, Fisher information matrix are studied. Estimates of the model parameters via method of maximum likelihood (ML), and method of moments (MOM) are presented for complete and censored data. Numerical examples are also presented.
entropy, Fisher information matrix are studied. Estimates of the model parameters via method of maximum likelihood (ML), and method of moments (MOM) are presented for complete and censored data. Numerical examples are also presented.References
Block, H. W., and Savits, T. H. (1998). The Reverse hazard Function, Probability in the Engineering and Informational Sciences,12, 69-90.
Calabria, R. and Pulcini, G. (1989). Confidence Limits for Reliability and Tolerance Limits in the Inverse Weibull Distribution, Engineering and System Safety, 24, 77-85 (1989).
Calabria, R. and Pulcini, G. (1990). On the Maximum Likelihood and Lease Squares Estimation in Inverse Weibull Distribution, Statistica Applicata, 2, 53-66.
Calabria, R. and Pulcini, G. (1994). Bayes 2-Sample Prediction for the Inverse Weibull Distribution, Communications in Statistics-Theory Meth., 23(6), 1811-1824.
Chandra, N. K. and Roy, D. (2001). Some results on Reverse Hazard Rate, Probability in the Engineering and Information Sciences, 15, 95-102.
Cordeiro, G. M., Ortega, E. M. and Nadarajah, S. (2010). The Kumaraswamy Weibull distribution with application to failure data, Journal of Franklin Institute, 347, 1399-1429.
Glaser, R. E. (1980). Bathtub and Related Failure Rate Characterizations, Journal of American Statistical Association, 75, 667-672.
Johnson, N. L., Kotz, S., and Balakrishnan, N. (1984). Continuous Univariate Distributions-1, Second Edition, John Wiley and Sons.
Jones, M. C. (2009). Kumaraswamy's distribution: a beta-type distribution with some tractability advantages, Statistical Methodology, 6, 70-91.
Keilson, J. and Sumita, U. (1982). Uniform Stochastic Ordering and Related Inequalities, Canadian Journal of Statistics, 10, 181-198.
Keller, A. Z., Giblin, M. T., and Farnworth, N.R. (1985). Reliability Analysis of Commercial Vehicle Engines, Reliability Engineering, 10, 15-25, 89-102.
Kumaraswamy, P. (1980). textit{Generalized probability density-function for double-bounded random-processes}, Journal of Hydrology, 46, 79-88.
Lawless, J. F. (2003). Statistical Models and Methods for Lifetime Date, Second Edition, John Wiley and Sons, Hoboken.
Lehmann, E. L. (1998). Theory of Point Estimation, Springer-Verlag New York, Inc.
Ross, S. M. (1983). Stochastic Processes, Wiley, New York.
Shaked, M. and Shanthikumar, J. G. (1994). Stochastic Orders and Their Applications, New York, Academic Press.
Zakerzadeh, H. and Dolati, A. (2009). Generalized Lindley Distribution, Journal of Mathematical Extension, 3, 13-25.
Full Text: pdf


