On locally homogeneous contact metric manifolds with Reeb flow invariant Jacobi operator
Abstract
We show that a locally homogeneous, regular contact metric manifold, whose characteristic Jacobi operator is invariant under the Reeb flow, is not compact, provided it admits at least one negative 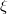 -sectional curvature.
-sectional curvature.
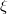 -sectional curvature.
-sectional curvature.DOI Code:
10.1285/i15900932v43n2p49
Keywords:
locally homogeneous contact metric manifold; regular contact manifold; characteristic Jacobi operator
Full Text: PDF


