Sequences of ideal norms
Abstract
There is a host of possibilities to associate with every (bounded linear) operator T, acting between Banach spaces, a scalar sequence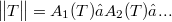 
such that all maps 
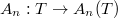are ideal norms. The asymptotic behaviour of 
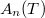as 
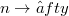can be used to define various subclasses of operatore. The most simple condition is that 
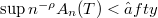where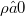 
. Tris yiehis a 1-parameter scale of Banach operator ideals. In what follows, this construction will be applied in some concrete cases. In particular, we let 
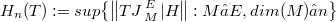where J{E \atop M} denotes the canonical embedding from the subspace M into E. Note that 
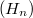is the natural dimensional gradation of the Hilbertian operator norm 
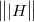in the sense of A. Pelczynski ([30], p. 165) and N. Tomczak-Jägermann ([46] and [48], p. 175). Taking the infimum over all 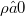with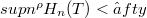 
we get an index ![h(T) ⊂ [0,1/2]](http://siba-ese.unisalento.it/plugins/generic/latexRender/cache/3f64110714a7813de02ccfdb77b5f74d.png)
which can be used to measure the <<Hilbertness>> of the operator T. Our main purpose is to show that several sequences of concrete ideal norms have the same asymptotic behaviour. This solves a problem posed in ([48],p. 210). We also give some applications to the geometry of Banach spaces. Conceming the basic definitions and various results from the theory of operator ideals, the reader is referred to my monographs [31] and [32]. The notation is adopted from the latter. The present paper is a revised and extended version of my preprint [36]. This revision became necessary when I observed that its main result was already contained in Remark 13.4 of G. Pisier's book [43]; see 5.3 below.
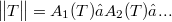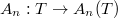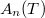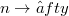such that all maps are ideal norms. The asymptotic behaviour of as can be used to define various subclasses of operatore. The most simple condition is that 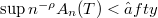where 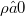. Tris yiehis a 1-parameter scale of Banach operator ideals. In what follows, this construction will be applied in some concrete cases. In particular, we let 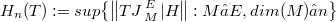where J{E \atop M} denotes the canonical embedding from the subspace M into E. Note that 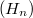is the natural dimensional gradation of the Hilbertian operator norm 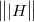in the sense of A. Pelczynski ([30], p. 165) and N. Tomczak-Jägermann ([46] and [48], p. 175). Taking the infimum over all 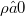with 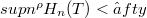we get an index which can be used to measure the <<Hilbertness>> of the operator T. Our main purpose is to show that several sequences of concrete ideal norms have the same asymptotic behaviour. This solves a problem posed in ([48],p. 210). We also give some applications to the geometry of Banach spaces. Conceming the basic definitions and various results from the theory of operator ideals, the reader is referred to my monographs [31] and [32]. The notation is adopted from the latter. The present paper is a revised and extended version of my preprint [36]. This revision became necessary when I observed that its main result was already contained in Remark 13.4 of G. Pisier's book [43]; see 5.3 below.DOI Code:
10.1285/i15900932v10supn2p411
Full Text: PDF
