Remarks on John's theorem on the ellipsoid of maximal volume inscribed into a convex symmetric body in Rn
Abstract
Relationships between some geometric properties of finite dimensional Banach spaces and distribution of contact points of the boundary of the unit ball of the space with the ellipsoid of maximal volume inscribed into the space are discussed. It is shown that every n-dimensional Banach space is isometrically isomorphic to a norm one complemented k-dimensional Banach space whose unit ball is affinely equivalent to a convex body which 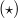 lies between the Euclidean unit ball and the standard cube circumscribed about the Euclidean unit hall, where
lies between the Euclidean unit ball and the standard cube circumscribed about the Euclidean unit hall, where 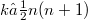 . Every n-dimensional space whose unit hall satisfies
. Every n-dimensional space whose unit hall satisfies 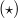 is within Banach-Mazur distance
is within Banach-Mazur distance 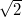 from some Banach space with the ball D whose boundary has
from some Banach space with the ball D whose boundary has 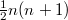 «equiweighted» contact points with the ellipsoid of maximal volume inscribed into D.
«equiweighted» contact points with the ellipsoid of maximal volume inscribed into D.
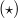 lies between the Euclidean unit ball and the standard cube circumscribed about the Euclidean unit hall, where
lies between the Euclidean unit ball and the standard cube circumscribed about the Euclidean unit hall, where 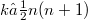 . Every n-dimensional space whose unit hall satisfies
. Every n-dimensional space whose unit hall satisfies 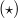 is within Banach-Mazur distance
is within Banach-Mazur distance 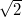 from some Banach space with the ball D whose boundary has
from some Banach space with the ball D whose boundary has 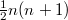 «equiweighted» contact points with the ellipsoid of maximal volume inscribed into D.
«equiweighted» contact points with the ellipsoid of maximal volume inscribed into D.DOI Code:
10.1285/i15900932v10supn2p395
Full Text: PDF


