A strict topology for some weighted spaces of continuous functions
Abstract
In the classical case the strict topology 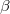 introduced by Buck [2] on the space
introduced by Buck [2] on the space 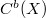 of bounded continuous scalar valued functions on the locally compact Hausdorff space X is given by the system W of all weights on X that vanish at infinity. The
of bounded continuous scalar valued functions on the locally compact Hausdorff space X is given by the system W of all weights on X that vanish at infinity. The 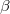 -bounded subsets of
-bounded subsets of 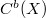 are exactly the norm bounded subsets, and
are exactly the norm bounded subsets, and 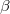 is the finest locally convex topology which coincides on the norm bounded subsets with the compact open topology (cf. Dorroh [4]). Especially we have that
is the finest locally convex topology which coincides on the norm bounded subsets with the compact open topology (cf. Dorroh [4]). Especially we have that 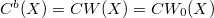 holds algebraically. In this note we want to describe for an arbitrary system of weights V an associated system of weights W such that at least in many cases, including the classical one, the connection between
holds algebraically. In this note we want to describe for an arbitrary system of weights V an associated system of weights W such that at least in many cases, including the classical one, the connection between 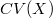 and
and 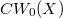 is the same as in the classical case.
is the same as in the classical case.
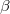 introduced by Buck [2] on the space
introduced by Buck [2] on the space 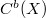 of bounded continuous scalar valued functions on the locally compact Hausdorff space X is given by the system W of all weights on X that vanish at infinity. The
of bounded continuous scalar valued functions on the locally compact Hausdorff space X is given by the system W of all weights on X that vanish at infinity. The  -bounded subsets of
-bounded subsets of  are exactly the norm bounded subsets, and
are exactly the norm bounded subsets, and 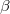 is the finest locally convex topology which coincides on the norm bounded subsets with the compact open topology (cf. Dorroh [4]). Especially we have that
is the finest locally convex topology which coincides on the norm bounded subsets with the compact open topology (cf. Dorroh [4]). Especially we have that 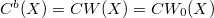 holds algebraically. In this note we want to describe for an arbitrary system of weights V an associated system of weights W such that at least in many cases, including the classical one, the connection between
holds algebraically. In this note we want to describe for an arbitrary system of weights V an associated system of weights W such that at least in many cases, including the classical one, the connection between 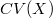 and
and 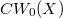 is the same as in the classical case.
is the same as in the classical case.DOI Code:
10.1285/i15900932v11p135
Full Text: PDF


