On the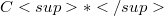 
-comparison algebra of a class of singular Sturm-Liouville expressions on the real line
Abstract
In this article we study a 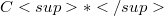-comparison algebra in the sense of [C2] with generators related to the ordinary differential expression H on the full real line R where,with constants 
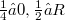, (1.1) (Error rendering LaTeX formula) More precisely, the algebra, called 
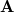, is generated by the multiplications 
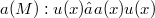, by functions ![a(x)∈ C([-∈fty,+∈fty])](http://siba-ese.unisalento.it/plugins/generic/latexRender/cache/4bf69a9089e497f2af147698034eceac.png)
and the (singular integral) operators(Error rendering LaTeX formula),and their adjoints. Here 
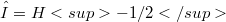, the inverse positive square root of the unique self-adjoint realization H of the expression (1.1), in the Hilbert space 
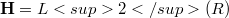.(We use the same notation for both, (1.1) and its realization.) The case of 
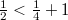was discussed earlier in [Tg1], even for all n-dimensional problem. The commutators are compact and the Fredholm properties of operators in 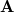are determined by a complex-valued symbol on a symbol space homeomorphic to that of the usual Laplace comparison algebra on 
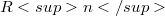, although the symbol itself is calculated by different formulas.
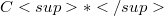-comparison algebra in the sense of [C2] with generators related to the ordinary differential expression H on the full real line R where,with constants 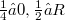, (1.1) (Error rendering LaTeX formula) More precisely, the algebra, called 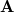, is generated by the multiplications 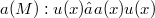, by functions and the (singular integral) operators(Error rendering LaTeX formula),and their adjoints. Here 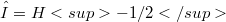, the inverse positive square root of the unique self-adjoint realization H of the expression (1.1), in the Hilbert space 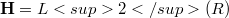.(We use the same notation for both, (1.1) and its realization.) The case of 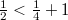was discussed earlier in [Tg1], even for all n-dimensional problem. The commutators are compact and the Fredholm properties of operators in 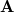are determined by a complex-valued symbol on a symbol space homeomorphic to that of the usual Laplace comparison algebra on 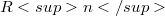, although the symbol itself is calculated by different formulas.DOI Code:
10.1285/i15900932v11p93
Full Text: PDF
