One-forms on spaces of embeddings: a frame work for constitutive laws in elasticity
Abstract
The present contribution to this volume is concerned with certain problems in non-linear functional analysis which are motivated by classical physics, specifically by elasticity theory:we are given a «body»,i.e. a compact smooth manifold 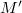 which moves and may be deformed in some
which moves and may be deformed in some 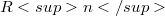 (equipped with a fixed inner product); we assume that the motion and deformation are such that the diffeomorphism type of
(equipped with a fixed inner product); we assume that the motion and deformation are such that the diffeomorphism type of 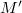 does not change. Hence,
does not change. Hence, 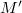 is the image under a smooth embedding of some compact smooth manifold M (possibly with boundary
is the image under a smooth embedding of some compact smooth manifold M (possibly with boundary 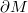 ) and the appropriate configuration space for the problem is the set
) and the appropriate configuration space for the problem is the set 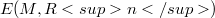 of smooth embeddings
of smooth embeddings 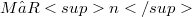 ; this set is a smooth Fréchet manifold when endowed with its natural
; this set is a smooth Fréchet manifold when endowed with its natural 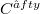 -topology.
-topology.
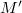 which moves and may be deformed in some
which moves and may be deformed in some 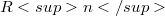 (equipped with a fixed inner product); we assume that the motion and deformation are such that the diffeomorphism type of
(equipped with a fixed inner product); we assume that the motion and deformation are such that the diffeomorphism type of 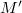 does not change. Hence,
does not change. Hence, 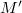 is the image under a smooth embedding of some compact smooth manifold M (possibly with boundary
is the image under a smooth embedding of some compact smooth manifold M (possibly with boundary 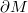 ) and the appropriate configuration space for the problem is the set
) and the appropriate configuration space for the problem is the set 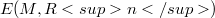 of smooth embeddings
of smooth embeddings 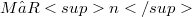 ; this set is a smooth Fréchet manifold when endowed with its natural
; this set is a smooth Fréchet manifold when endowed with its natural 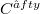 -topology.
-topology.DOI Code:
10.1285/i15900932v11p21
Full Text: PDF


