On the Action of 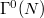 on
on 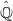
Abstract
In this paper we examine 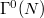 -orbits on
-orbits on 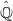 and the suborbital graphs for
and the suborbital graphs for 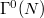 . Each such suborbitalgraph is a disjoint union of subgraphs whose vertices form a blockof imprimitivity for
. Each such suborbitalgraph is a disjoint union of subgraphs whose vertices form a blockof imprimitivity for 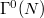 . Moreover, these subgraphs areshown to be vertex
. Moreover, these subgraphs areshown to be vertex 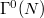 -transitive and edge
-transitive and edge 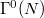 -transitive. Finally, necessary and sufficient conditions forbeing self-paired edge are provided.
-transitive. Finally, necessary and sufficient conditions forbeing self-paired edge are provided.
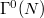 -orbits on
-orbits on 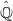 and the suborbital graphs for
and the suborbital graphs for 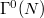 . Each such suborbitalgraph is a disjoint union of subgraphs whose vertices form a blockof imprimitivity for
. Each such suborbitalgraph is a disjoint union of subgraphs whose vertices form a blockof imprimitivity for 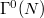 . Moreover, these subgraphs areshown to be vertex
. Moreover, these subgraphs areshown to be vertex 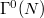 -transitive and edge
-transitive and edge 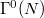 -transitive. Finally, necessary and sufficient conditions forbeing self-paired edge are provided.
-transitive. Finally, necessary and sufficient conditions forbeing self-paired edge are provided.DOI Code:
10.1285/i15900932v30n2p141
Keywords:
Congruence groups; Transitive and Imprimitive action; Suborbital graphs
Full Text: PDF


