Characterizations by normal coordinates of special points and conics of a triangle
Abstract
In (6), we associated with a given triangle 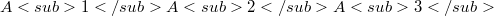 and with each point P of the Euclidean plane a pencil of homothethic ellipses or hyperbolas with center P, which are determined by the loci of the points of the plane for which the distances
and with each point P of the Euclidean plane a pencil of homothethic ellipses or hyperbolas with center P, which are determined by the loci of the points of the plane for which the distances 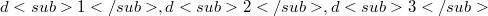 to the sides of the triangle
to the sides of the triangle 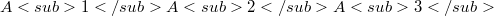 are related by(Error rendering LaTeX formula) (s variable in
are related by(Error rendering LaTeX formula) (s variable in 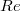 ),where
),where 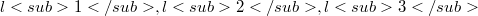 are the lengths of the sides of the triangle and where(Error rendering LaTeX formula) are normal coordinates of P relative to the triangle
are the lengths of the sides of the triangle and where(Error rendering LaTeX formula) are normal coordinates of P relative to the triangle 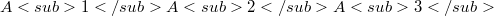 (see section 1). In particular, a construction for the axes of these conics is given. Several special cases are treated, where P is the orthocenter H, the Lemoine point K, the incenter I, the centroid Z, and the circumcenter O of
(see section 1). In particular, a construction for the axes of these conics is given. Several special cases are treated, where P is the orthocenter H, the Lemoine point K, the incenter I, the centroid Z, and the circumcenter O of 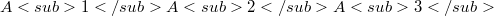 (for a summary of these results, see section 2). In the present paper, we construct another pencil of conics with center P, using again normal coordinates relative to
(for a summary of these results, see section 2). In the present paper, we construct another pencil of conics with center P, using again normal coordinates relative to 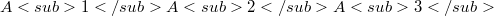 and look again for the axes, especially in the cases where P = H, K, I, Z, or O.
and look again for the axes, especially in the cases where P = H, K, I, Z, or O.
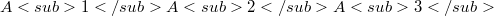 and with each point P of the Euclidean plane a pencil of homothethic ellipses or hyperbolas with center P, which are determined by the loci of the points of the plane for which the distances
and with each point P of the Euclidean plane a pencil of homothethic ellipses or hyperbolas with center P, which are determined by the loci of the points of the plane for which the distances 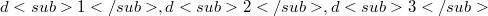 to the sides of the triangle
to the sides of the triangle 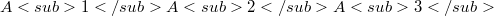 are related by(Error rendering LaTeX formula) (s variable in
are related by(Error rendering LaTeX formula) (s variable in 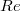 ),where
),where 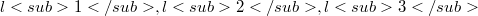 are the lengths of the sides of the triangle and where(Error rendering LaTeX formula) are normal coordinates of P relative to the triangle
are the lengths of the sides of the triangle and where(Error rendering LaTeX formula) are normal coordinates of P relative to the triangle 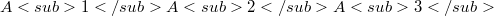 (see section 1). In particular, a construction for the axes of these conics is given. Several special cases are treated, where P is the orthocenter H, the Lemoine point K, the incenter I, the centroid Z, and the circumcenter O of
(see section 1). In particular, a construction for the axes of these conics is given. Several special cases are treated, where P is the orthocenter H, the Lemoine point K, the incenter I, the centroid Z, and the circumcenter O of 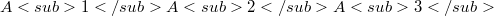 (for a summary of these results, see section 2). In the present paper, we construct another pencil of conics with center P, using again normal coordinates relative to
(for a summary of these results, see section 2). In the present paper, we construct another pencil of conics with center P, using again normal coordinates relative to 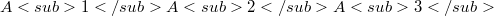 and look again for the axes, especially in the cases where P = H, K, I, Z, or O.
and look again for the axes, especially in the cases where P = H, K, I, Z, or O.DOI Code:
10.1285/i15900932v24n1p9
Keywords:
Euclidean plane; Triangle center; Trilinear coordinates
Classification:
51N20; 51M04
Full Text: PDF


