When may two systems of orthonormal functions be interchanged in vector-valued orthogonal sums?
Abstract
Given a finite orthonormal sequence(Error rendering LaTeX formula) in some 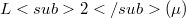 and vectors
and vectors 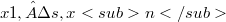 in some Banach space X we are interested in the norm of the sums(Error rendering LaTeX formula) in
in some Banach space X we are interested in the norm of the sums(Error rendering LaTeX formula) in 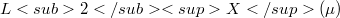 .A constuction in [1] suggests that the system
.A constuction in [1] suggests that the system 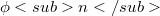 may be replaced by the set(Error rendering LaTeX formula) of coordinate functions(Error rendering LaTeX formula) on
may be replaced by the set(Error rendering LaTeX formula) of coordinate functions(Error rendering LaTeX formula) on 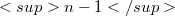 viewed as un orthonormal system with respect to a suitable measure λ on
viewed as un orthonormal system with respect to a suitable measure λ on 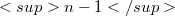 .We show by a convolutional argument that after symmetrization the measure λ is uniquely determined.We also discuss related questions.
.We show by a convolutional argument that after symmetrization the measure λ is uniquely determined.We also discuss related questions.
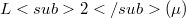 and vectors
and vectors 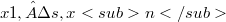 in some Banach space X we are interested in the norm of the sums(Error rendering LaTeX formula) in
in some Banach space X we are interested in the norm of the sums(Error rendering LaTeX formula) in 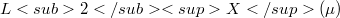 .A constuction in [1] suggests that the system
.A constuction in [1] suggests that the system 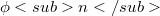 may be replaced by the set(Error rendering LaTeX formula) of coordinate functions(Error rendering LaTeX formula) on
may be replaced by the set(Error rendering LaTeX formula) of coordinate functions(Error rendering LaTeX formula) on 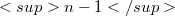 viewed as un orthonormal system with respect to a suitable measure λ on
viewed as un orthonormal system with respect to a suitable measure λ on 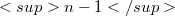 .We show by a convolutional argument that after symmetrization the measure λ is uniquely determined.We also discuss related questions.
.We show by a convolutional argument that after symmetrization the measure λ is uniquely determined.We also discuss related questions.DOI Code:
10.1285/i15900932v16n1p47
Full Text: PDF


