Decompositions of Montel Köthe sequence spaces
Abstract
The following result has been recently proved by the author: Let E be a Fréchet Schwartz space with unconditional basis and with continuous norm; let F be any infinite dimensional subspace of E. Then we can write E as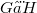 
where G and H do not have any subspace isomorphic to F. This theorem is extended here in two directions: (i)If E is a Montel Köthe sequence space (with certain additional assumptions which are satisfied by the examples described in the literature) and the subspace F is Montel non-Schwartz; (ii) If E is any Fréchet Schwartz space with unconditional basis (so the existence of continuous norm is dropped) and F is not isomorphic to 
.
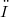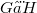where G and H do not have any subspace isomorphic to F. This theorem is extended here in two directions: (i)If E is a Montel Köthe sequence space (with certain additional assumptions which are satisfied by the examples described in the literature) and the subspace F is Montel non-Schwartz; (ii) If E is any Fréchet Schwartz space with unconditional basis (so the existence of continuous norm is dropped) and F is not isomorphic to 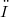.DOI Code:
10.1285/i15900932v17p143
Keywords:
Köthe sequence spaces; Primary spaces; Complemented subspaces; Countable products of Fréchet Schwartz spaces
Classification:
46A45; 46A01; 46A11
Full Text: PDF
