On dense subspaces of Cp(X)
Abstract
For a Tychonoff space X, we denote by Cp(X) the space of all real-valued continuous functions on X with the topology of pointwise convergence. We show the following:(1) if ω1 is a caliber for every dense subspace of Cp(X), then Cp X) is (ω1, ω1)-narrow; (2) if every dense subspace of Cp(X) is compact-dense in Cp(X), then every non-trivial countable 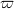 -cover of open sets of X contains a γ-cover. The first result gives the positive answer to Problem 4.4 in [6], and the second one is a partial answer to Problem 4.3 in [6].
-cover of open sets of X contains a γ-cover. The first result gives the positive answer to Problem 4.4 in [6], and the second one is a partial answer to Problem 4.3 in [6].
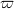 -cover of open sets of X contains a γ-cover. The first result gives the positive answer to Problem 4.4 in [6], and the second one is a partial answer to Problem 4.3 in [6].
-cover of open sets of X contains a γ-cover. The first result gives the positive answer to Problem 4.4 in [6], and the second one is a partial answer to Problem 4.3 in [6].DOI Code:
10.1285/i15900932v27supn1p41
Keywords:
Function space; Dense subspace; Caliber; (k, k)-compact; (k, k)-narrow; Linearly Lindelöf; ω-cover; γ-cover; Fréchet
Classification:
54C35; 54D20
Full Text: PDF


