Canonical Reductive Decomposition of Extrinsic Homogeneous Submanifolds
Abstract
Let 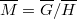 be a homogeneous Riemannian manifold. Given a Lie subgroup
be a homogeneous Riemannian manifold. Given a Lie subgroup 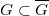 and a reductive decomposition of the homogeneous structure of
and a reductive decomposition of the homogeneous structure of 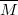 , we analyze a canonical reductive decomposition for the orbits of the action of
, we analyze a canonical reductive decomposition for the orbits of the action of 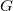 . These leaves of the
. These leaves of the 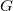 -action are extrinsic homogeneous submanifolds and the analysis of the reductive decomposition of them is related with their extrinsic properties. We connect the study with works in the literature and initiate the relationship with the Ambrose-Singer theorem and homogeneous structures of submanifolds.
-action are extrinsic homogeneous submanifolds and the analysis of the reductive decomposition of them is related with their extrinsic properties. We connect the study with works in the literature and initiate the relationship with the Ambrose-Singer theorem and homogeneous structures of submanifolds.
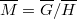 be a homogeneous Riemannian manifold. Given a Lie subgroup
be a homogeneous Riemannian manifold. Given a Lie subgroup 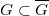 and a reductive decomposition of the homogeneous structure of
and a reductive decomposition of the homogeneous structure of 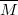 , we analyze a canonical reductive decomposition for the orbits of the action of
, we analyze a canonical reductive decomposition for the orbits of the action of 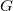 . These leaves of the
. These leaves of the 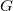 -action are extrinsic homogeneous submanifolds and the analysis of the reductive decomposition of them is related with their extrinsic properties. We connect the study with works in the literature and initiate the relationship with the Ambrose-Singer theorem and homogeneous structures of submanifolds.
-action are extrinsic homogeneous submanifolds and the analysis of the reductive decomposition of them is related with their extrinsic properties. We connect the study with works in the literature and initiate the relationship with the Ambrose-Singer theorem and homogeneous structures of submanifolds.DOI Code:
10.1285/i15900932v45s1p117
Keywords:
Ambrose-Singer theorem; extrinsic homogeneity; reductive decomposition
Full Text: PDF


