BGG Sequences | A Riemannian perspective
Abstract
BGG resolutions and generalized BGG resolutions from representation theory of semisimple Lie algebras have been generalized to sequences of invariant differential operators on manifolds endowed with a geometric structure belonging to the family of parabolic geometries. Two of these structures, occur as conformal structures and projective structures occur as weakenings of a Riemannian metric respectively of a specified torsion-free connection on the tangent bundle. In particular, one obtains BGG sequences on open subsets of 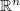 as very special cases of the construction. It turned out that several examples of the latter sequences are of interest in applied mathematics, since they can be used to construct numerical methods to study operators relevant for elasticity theory, numerical relativity and related fields. This article is intended to provide an intermediate level between BGG sequences for parabolic geometries and the case of domains in
as very special cases of the construction. It turned out that several examples of the latter sequences are of interest in applied mathematics, since they can be used to construct numerical methods to study operators relevant for elasticity theory, numerical relativity and related fields. This article is intended to provide an intermediate level between BGG sequences for parabolic geometries and the case of domains in 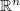 . We provide a construction of conformal BGG sequences on Riemannian manifolds and of projective BGG sequences on manifolds endowed with a volume preserving linear connection on their tangent bundle. These constructions do not need any input from parabolic geometries. Except from standard differential geometry methods the only deeper input comes from representation theory. So one can either view the results as a simplified version of the constructions for parabolic geometries in an explicit form. Alternatively, one can view them as providing an extension of the simplified constructions for domains in
. We provide a construction of conformal BGG sequences on Riemannian manifolds and of projective BGG sequences on manifolds endowed with a volume preserving linear connection on their tangent bundle. These constructions do not need any input from parabolic geometries. Except from standard differential geometry methods the only deeper input comes from representation theory. So one can either view the results as a simplified version of the constructions for parabolic geometries in an explicit form. Alternatively, one can view them as providing an extension of the simplified constructions for domains in 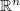 to general Riemannian manifolds or to manifolds endowed with an appropriate connection on the tangent bundle.
to general Riemannian manifolds or to manifolds endowed with an appropriate connection on the tangent bundle.
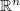 as very special cases of the construction. It turned out that several examples of the latter sequences are of interest in applied mathematics, since they can be used to construct numerical methods to study operators relevant for elasticity theory, numerical relativity and related fields. This article is intended to provide an intermediate level between BGG sequences for parabolic geometries and the case of domains in
as very special cases of the construction. It turned out that several examples of the latter sequences are of interest in applied mathematics, since they can be used to construct numerical methods to study operators relevant for elasticity theory, numerical relativity and related fields. This article is intended to provide an intermediate level between BGG sequences for parabolic geometries and the case of domains in 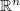 . We provide a construction of conformal BGG sequences on Riemannian manifolds and of projective BGG sequences on manifolds endowed with a volume preserving linear connection on their tangent bundle. These constructions do not need any input from parabolic geometries. Except from standard differential geometry methods the only deeper input comes from representation theory. So one can either view the results as a simplified version of the constructions for parabolic geometries in an explicit form. Alternatively, one can view them as providing an extension of the simplified constructions for domains in
. We provide a construction of conformal BGG sequences on Riemannian manifolds and of projective BGG sequences on manifolds endowed with a volume preserving linear connection on their tangent bundle. These constructions do not need any input from parabolic geometries. Except from standard differential geometry methods the only deeper input comes from representation theory. So one can either view the results as a simplified version of the constructions for parabolic geometries in an explicit form. Alternatively, one can view them as providing an extension of the simplified constructions for domains in 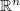 to general Riemannian manifolds or to manifolds endowed with an appropriate connection on the tangent bundle.
to general Riemannian manifolds or to manifolds endowed with an appropriate connection on the tangent bundle.DOI Code:
10.1285/i15900932v45s1p83
Keywords:
Bernstein-Gelfand-Gelfand sequences; BGG sequences; BGG machinery; geometric prolongation; invariant differential operators
Full Text: PDF


