On the local spectral subspace preservers Youssef Bouramdane
Abstract
Let  be the algebra of all bounded linear operators on a complex Banach space
be the algebra of all bounded linear operators on a complex Banach space 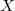 with
with 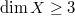 . In this paper, we characterize the maps from
. In this paper, we characterize the maps from  into itself which preserves the dimension of the local spectral subspace relative to
into itself which preserves the dimension of the local spectral subspace relative to  of the product of operators. The form of the maps from
of the product of operators. The form of the maps from  into itself preserving the local spectral subspace relative to
into itself preserving the local spectral subspace relative to  of the product of operators are also described.
of the product of operators are also described.
 be the algebra of all bounded linear operators on a complex Banach space
be the algebra of all bounded linear operators on a complex Banach space 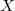 with
with 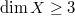 . In this paper, we characterize the maps from
. In this paper, we characterize the maps from  into itself which preserves the dimension of the local spectral subspace relative to
into itself which preserves the dimension of the local spectral subspace relative to  of the product of operators. The form of the maps from
of the product of operators. The form of the maps from  into itself preserving the local spectral subspace relative to
into itself preserving the local spectral subspace relative to  of the product of operators are also described.
of the product of operators are also described.DOI Code:
10.1285/i15900932v45n1p81
Keywords:
local spectral subspace; preserver problem; operator algebra
Full Text: PDF


