Construction of a function using its values along 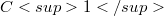 curves
curves
Abstract
Let 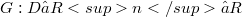 be a function. Any parametrized curve 𝛼 in D determines the composition
be a function. Any parametrized curve 𝛼 in D determines the composition 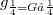 . If 𝛼 belongs to a family of curves, the family
. If 𝛼 belongs to a family of curves, the family 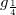 satisfies some conditions. Our goal is to find the conditions in which the families {𝛼},
satisfies some conditions. Our goal is to find the conditions in which the families {𝛼}, 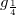 determine the function G. Section 1 emphasizes the origin of the problem. Section 2 defines and studies the notion of the Γ function. Section 3 presents the construction of a function using a Γ-function.
determine the function G. Section 1 emphasizes the origin of the problem. Section 2 defines and studies the notion of the Γ function. Section 3 presents the construction of a function using a Γ-function.
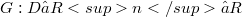 be a function. Any parametrized curve 𝛼 in D determines the composition
be a function. Any parametrized curve 𝛼 in D determines the composition 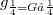 . If 𝛼 belongs to a family of curves, the family
. If 𝛼 belongs to a family of curves, the family 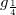 satisfies some conditions. Our goal is to find the conditions in which the families {𝛼},
satisfies some conditions. Our goal is to find the conditions in which the families {𝛼}, 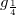 determine the function G. Section 1 emphasizes the origin of the problem. Section 2 defines and studies the notion of the Γ function. Section 3 presents the construction of a function using a Γ-function.
determine the function G. Section 1 emphasizes the origin of the problem. Section 2 defines and studies the notion of the Γ function. Section 3 presents the construction of a function using a Γ-function.DOI Code:
10.1285/i15900932v27n1p131
Keywords:
Extension of maps; Function spaces; Γ-function; Generated functions
Full Text: PDF PS


