Investigation of some special tensor fields on space-times with holonomy algebras
Abstract
This paper studies the concircular, projective and conharmonic curvature tensors on 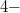 dimensional Lorentzian manifolds known as space-times. We obtain some properties of these tensor fields by relating the known holonomy algebras for Lorentz signature
dimensional Lorentzian manifolds known as space-times. We obtain some properties of these tensor fields by relating the known holonomy algebras for Lorentz signature 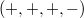 . For the space-times admitting special vector fields, such as parallel and recurrent vector fields, some theorems are proved. The eigenbivector structure of the investigated tensor fields is also examined in these spaces. These results obtained by considering the holonomy theory are associated with the algebraic classification of the Riemann curvature and Ricci tensors for Lorentz signature, and various examples related to the study are also given.
. For the space-times admitting special vector fields, such as parallel and recurrent vector fields, some theorems are proved. The eigenbivector structure of the investigated tensor fields is also examined in these spaces. These results obtained by considering the holonomy theory are associated with the algebraic classification of the Riemann curvature and Ricci tensors for Lorentz signature, and various examples related to the study are also given.
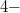 dimensional Lorentzian manifolds known as space-times. We obtain some properties of these tensor fields by relating the known holonomy algebras for Lorentz signature
dimensional Lorentzian manifolds known as space-times. We obtain some properties of these tensor fields by relating the known holonomy algebras for Lorentz signature 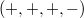 . For the space-times admitting special vector fields, such as parallel and recurrent vector fields, some theorems are proved. The eigenbivector structure of the investigated tensor fields is also examined in these spaces. These results obtained by considering the holonomy theory are associated with the algebraic classification of the Riemann curvature and Ricci tensors for Lorentz signature, and various examples related to the study are also given.
. For the space-times admitting special vector fields, such as parallel and recurrent vector fields, some theorems are proved. The eigenbivector structure of the investigated tensor fields is also examined in these spaces. These results obtained by considering the holonomy theory are associated with the algebraic classification of the Riemann curvature and Ricci tensors for Lorentz signature, and various examples related to the study are also given.DOI Code:
10.1285/i15900932v43n2p83
Keywords:
concircular curvature tensor; projective curvature tensor; conharmonic curvature tensor; holonomy; Lorentz signature
Full Text: PDF


