On an autoregressive process driven by a sequence of Gaussian cylindrical random variables
Abstract
Let 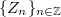 be a sequence of identically distributed, weakly independent and weakly Gaussian cylindrical random variables in a separable Banach space
be a sequence of identically distributed, weakly independent and weakly Gaussian cylindrical random variables in a separable Banach space 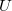 . We consider the cylindrical difference equation,
. We consider the cylindrical difference equation, 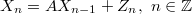 , in
, in 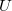 and determine a cylindrical process
and determine a cylindrical process 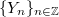 which solves the equation. The cylindrical distribution of
which solves the equation. The cylindrical distribution of 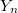 is shown to be weakly Gaussian and independent of
is shown to be weakly Gaussian and independent of  . It is also shown to be strongly Gaussian if the cylindrical distribution of
. It is also shown to be strongly Gaussian if the cylindrical distribution of 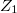 is strongly Gaussian. We determine the characteristic functional of
is strongly Gaussian. We determine the characteristic functional of 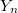 and give conditions under which
and give conditions under which 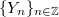 is unique.
is unique.
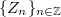 be a sequence of identically distributed, weakly independent and weakly Gaussian cylindrical random variables in a separable Banach space
be a sequence of identically distributed, weakly independent and weakly Gaussian cylindrical random variables in a separable Banach space 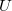 . We consider the cylindrical difference equation,
. We consider the cylindrical difference equation, 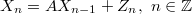 , in
, in 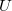 and determine a cylindrical process
and determine a cylindrical process 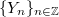 which solves the equation. The cylindrical distribution of
which solves the equation. The cylindrical distribution of 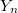 is shown to be weakly Gaussian and independent of
is shown to be weakly Gaussian and independent of  . It is also shown to be strongly Gaussian if the cylindrical distribution of
. It is also shown to be strongly Gaussian if the cylindrical distribution of 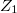 is strongly Gaussian. We determine the characteristic functional of
is strongly Gaussian. We determine the characteristic functional of 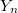 and give conditions under which
and give conditions under which 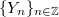 is unique.
is unique.DOI Code:
10.1285/i15900932v41n1p111
Keywords:
Autoregressive process; Cylindrical process; Cylindrical measure; Cylindrical random variable; Stationary process
Full Text: PDF


