On the edge metric dimension and Wiener index of the blow up of graphs
Abstract
Let 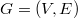 be a connected graph. The distance between an edge
be a connected graph. The distance between an edge 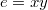 and a vertex
and a vertex  is defined as
is defined as 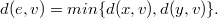 A nonempty set
A nonempty set 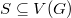 is an edge metric generator for
is an edge metric generator for  if for any two distinct edges
if for any two distinct edges 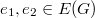 , there exists a vertex
, there exists a vertex 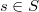 such that
such that 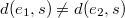 . An edge metric generating set with the smallest number of elements is called an edge metric basis of
. An edge metric generating set with the smallest number of elements is called an edge metric basis of  , and the number of elements in an edge metric basis is called the edge metric dimension of
, and the number of elements in an edge metric basis is called the edge metric dimension of  and it is denoted by
and it is denoted by 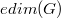 . In this paper, we study the edge metric dimension of a blow up of a graph
. In this paper, we study the edge metric dimension of a blow up of a graph  , and also we study the edge metric dimension of the zero divisor graph of the ring of integers modulo
, and also we study the edge metric dimension of the zero divisor graph of the ring of integers modulo  . Moreover, the Wiener index and the hyper-Wiener index of the blow up of certain graphs are computed.
. Moreover, the Wiener index and the hyper-Wiener index of the blow up of certain graphs are computed.
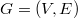 be a connected graph. The distance between an edge
be a connected graph. The distance between an edge 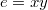 and a vertex
and a vertex  is defined as
is defined as 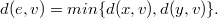 A nonempty set
A nonempty set 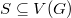 is an edge metric generator for
is an edge metric generator for  if for any two distinct edges
if for any two distinct edges 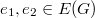 , there exists a vertex
, there exists a vertex 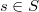 such that
such that 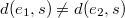 . An edge metric generating set with the smallest number of elements is called an edge metric basis of
. An edge metric generating set with the smallest number of elements is called an edge metric basis of  , and the number of elements in an edge metric basis is called the edge metric dimension of
, and the number of elements in an edge metric basis is called the edge metric dimension of  and it is denoted by
and it is denoted by 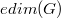 . In this paper, we study the edge metric dimension of a blow up of a graph
. In this paper, we study the edge metric dimension of a blow up of a graph  , and also we study the edge metric dimension of the zero divisor graph of the ring of integers modulo
, and also we study the edge metric dimension of the zero divisor graph of the ring of integers modulo  . Moreover, the Wiener index and the hyper-Wiener index of the blow up of certain graphs are computed.
. Moreover, the Wiener index and the hyper-Wiener index of the blow up of certain graphs are computed.DOI Code:
10.1285/i15900932v40n2p99
Keywords:
Edge metric dimension; Wiener index; Hyper-Wiener index; Blow up of a graph; Zero divisor graph
Full Text: PDF


