Adjoint symmetries for graded vector fields
Abstract
Suppose that 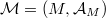 is a graded manifold and consider a direct subsheaf
is a graded manifold and consider a direct subsheaf  of
of 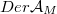 and a graded vector field
and a graded vector field 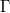 on
on 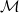 , both satisfying certain conditions.
, both satisfying certain conditions.  is used to characterize the local expression of
is used to characterize the local expression of 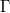 . Thus we review some of the basic definitions, properties, and geometric structures related to the theory of adjoint symmetries on a graded manifold and discuss some ideas from Lagrangian supermechanics in an informal fashion. In the special case where
. Thus we review some of the basic definitions, properties, and geometric structures related to the theory of adjoint symmetries on a graded manifold and discuss some ideas from Lagrangian supermechanics in an informal fashion. In the special case where 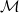 is the tangent supermanifold, we are able to find a generalization of the adjoint symmetry method for time-dependent second-order equations to the graded case. Finally, the relationship between adjoint symmetries of
is the tangent supermanifold, we are able to find a generalization of the adjoint symmetry method for time-dependent second-order equations to the graded case. Finally, the relationship between adjoint symmetries of 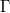 and Lagrangians is studied.
and Lagrangians is studied.
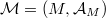 is a graded manifold and consider a direct subsheaf
is a graded manifold and consider a direct subsheaf  of
of 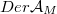 and a graded vector field
and a graded vector field 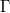 on
on 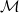 , both satisfying certain conditions.
, both satisfying certain conditions.  is used to characterize the local expression of
is used to characterize the local expression of 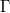 . Thus we review some of the basic definitions, properties, and geometric structures related to the theory of adjoint symmetries on a graded manifold and discuss some ideas from Lagrangian supermechanics in an informal fashion. In the special case where
. Thus we review some of the basic definitions, properties, and geometric structures related to the theory of adjoint symmetries on a graded manifold and discuss some ideas from Lagrangian supermechanics in an informal fashion. In the special case where 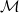 is the tangent supermanifold, we are able to find a generalization of the adjoint symmetry method for time-dependent second-order equations to the graded case. Finally, the relationship between adjoint symmetries of
is the tangent supermanifold, we are able to find a generalization of the adjoint symmetry method for time-dependent second-order equations to the graded case. Finally, the relationship between adjoint symmetries of 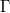 and Lagrangians is studied.
and Lagrangians is studied.DOI Code:
10.1285/i15900932v39n1p33
Keywords:
supermanifold; involutive distribution; second-order differential equation field; Lagrangian systems; adjoint symmetry
Full Text: PDF


