On a conjecture about the autotopism group of the Figueroa's presemifields of order 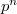
Abstract
In [14] was proved that the autotopism group of the Cordero-Figueroa semifield of order 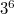 is isomorphic to a subgroup of
is isomorphic to a subgroup of 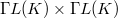 , where
, where 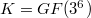 . Also a conjecture was proposed for the general case, the autotopism group of a Figueroa's presemifield of order
. Also a conjecture was proposed for the general case, the autotopism group of a Figueroa's presemifield of order 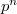 . In this article, under a normality condition, we prove this conjecture.
. In this article, under a normality condition, we prove this conjecture.
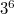 is isomorphic to a subgroup of
is isomorphic to a subgroup of 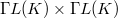 , where
, where 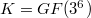 . Also a conjecture was proposed for the general case, the autotopism group of a Figueroa's presemifield of order
. Also a conjecture was proposed for the general case, the autotopism group of a Figueroa's presemifield of order 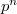 . In this article, under a normality condition, we prove this conjecture.
. In this article, under a normality condition, we prove this conjecture.DOI Code:
10.1285/i15900932v38n2p11
Keywords:
finite presemifield; finite semifield; autotopism; autotopism group; Cordero-Figueroa semifield; Figueroa's presemifields
Full Text: PDF


