A spaceability result in the context of hypergroups
Abstract
In this paper, by an elementary constractive technique, it is shown that 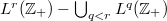 is non-empty, where
is non-empty, where 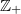 is the dual of a compact countable hypergroup introduced by Dunkl and Ramirez. Also, we prove that for each
is the dual of a compact countable hypergroup introduced by Dunkl and Ramirez. Also, we prove that for each 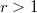 ,
, 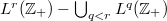 is spaceable.
is spaceable.
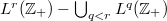 is non-empty, where
is non-empty, where 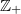 is the dual of a compact countable hypergroup introduced by Dunkl and Ramirez. Also, we prove that for each
is the dual of a compact countable hypergroup introduced by Dunkl and Ramirez. Also, we prove that for each 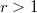 ,
, 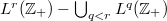 is spaceable.
is spaceable.DOI Code:
10.1285/i15900932v38n1p17
Keywords:
locally compact hypergroup; spaceability; $L^p$-space
Full Text: PDF


