The State of the Art on the Conjecture of Exceptional APN Functions
Abstract
The well known conjecture about exceptional almost perfect non-linear (exceptional APN) functions, stated by Aubry, McGuire and Rodier, says that the monomials 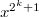 and
and 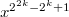 , the Gold and Kasami-Welch functions respectively, are the only ones in this class. Many results have been obtained in the last years confirming the conjecture. In this article we list all these settled results, all the pending cases, and provide a new family of non exceptional APN functions. Also, we comment the methods used to obtain the resolved cases and propose a provable new one, using the Max Noether's Fundamental theorem, to overcome some pending cases.
, the Gold and Kasami-Welch functions respectively, are the only ones in this class. Many results have been obtained in the last years confirming the conjecture. In this article we list all these settled results, all the pending cases, and provide a new family of non exceptional APN functions. Also, we comment the methods used to obtain the resolved cases and propose a provable new one, using the Max Noether's Fundamental theorem, to overcome some pending cases.
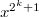 and
and 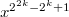 , the Gold and Kasami-Welch functions respectively, are the only ones in this class. Many results have been obtained in the last years confirming the conjecture. In this article we list all these settled results, all the pending cases, and provide a new family of non exceptional APN functions. Also, we comment the methods used to obtain the resolved cases and propose a provable new one, using the Max Noether's Fundamental theorem, to overcome some pending cases.
, the Gold and Kasami-Welch functions respectively, are the only ones in this class. Many results have been obtained in the last years confirming the conjecture. In this article we list all these settled results, all the pending cases, and provide a new family of non exceptional APN functions. Also, we comment the methods used to obtain the resolved cases and propose a provable new one, using the Max Noether's Fundamental theorem, to overcome some pending cases.DOI Code:
10.1285/i15900932v37n1p41
Keywords:
Almost perfect nonlinear; exceptional almost perfect nonlinear; absolute irreducibility; bezout's theorem; Max Noether's theorem
Full Text: PDF


