Generalized Fourier expansions for zero-solutions of surjective convolution operators on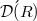 
and 
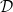
Abstract
It is well-known that each distribution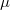 
with compact support can be convolved with an arbitrary distribution and that this defines a convolution operator 
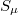, acting on 
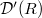.The surjectivity of 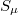, was characterized by Ehrenpreis [5]. Extending this result,we characterize in the present article the surjectivity of convolution operators on the space 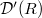of all w-ultradistributions of Beurling type on R.This is done in two steps. In the first one we show that 
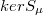has an absolute basis whenever 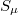, admits a fundamental solution 
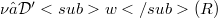. The expansion of an element in 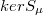, with respect to this basis can be regarded as a generalization of the Fourier expansion of periodic ultradistributions.In the second step we use this sequence space representation together with results of Palamodov [15] and Vogt [17], [18] on the projective limit functor to obtain the desired characterization.It turns out that 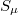is surjective if and only if 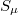admits a fundamental solution. 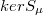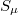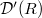Hence the elements of admit a generalized Fourier expansion for each surjective convolution operator on .Note that this differs from the behavior of convolution operators on the space 
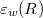of w-ultradifferentiable functions of Roumieu-type, as Braun,Meise and Vogt [4] have shown. Note also that the results of the present article apply to convolution operators on 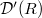,too.
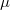with compact support can be convolved with an arbitrary distribution and that this defines a convolution operator 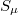, acting on 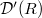.The surjectivity of 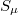, was characterized by Ehrenpreis [5]. Extending this result,we characterize in the present article the surjectivity of convolution operators on the space 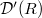of all w-ultradistributions of Beurling type on R.This is done in two steps. In the first one we show that 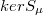has an absolute basis whenever 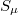, admits a fundamental solution 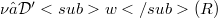. The expansion of an element in 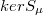, with respect to this basis can be regarded as a generalization of the Fourier expansion of periodic ultradistributions.In the second step we use this sequence space representation together with results of Palamodov [15] and Vogt [17], [18] on the projective limit functor to obtain the desired characterization.It turns out that 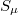is surjective if and only if 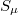admits a fundamental solution. 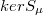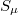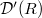Hence the elements of admit a generalized Fourier expansion for each surjective convolution operator on .Note that this differs from the behavior of convolution operators on the space 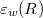of w-ultradifferentiable functions of Roumieu-type, as Braun,Meise and Vogt [4] have shown. Note also that the results of the present article apply to convolution operators on 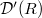,too.DOI Code:
10.1285/i15900932v10supn1p251
Full Text: PDF
