Ashort proof of Alexandrov-Fenchel\'s inequality
Abstract
More than half a century ago Alexandrov [1] and Fenchel [8] proved a generalization of Minkowski's inequalities on volume and surface area of convex bodies: Let 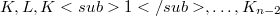 be convex bodies in
be convex bodies in 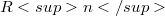 , and let
, and let 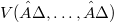 denote mixed volume. Then (AF) (Error rendering LaTeX formula) (For proofs see also Busemann [4], and Leichtweiss [9]). New interest in (AF)has been stimulated recently, partly by the discovery of its equivalence with the Hodge inequality in case of compact projective toric varieties (see Teissier [13], Khovanskij in Burago-Zalgaller [3]).The problem of characterizing equality in (AF) is still unsolved, though progress has been made during the last five years by R. Schneider ([10], [11], [12]),E. Tondorf, and the author ([5], [6], [7]. The method we have introduced hereby in [5] has meanwhile turned out to be applicable to a short and relatively elementary proof of (AF); we present it in this note. We are hopeful it will also contributed to a better understanding of (AF) and open problems connected with the inequality.
denote mixed volume. Then (AF) (Error rendering LaTeX formula) (For proofs see also Busemann [4], and Leichtweiss [9]). New interest in (AF)has been stimulated recently, partly by the discovery of its equivalence with the Hodge inequality in case of compact projective toric varieties (see Teissier [13], Khovanskij in Burago-Zalgaller [3]).The problem of characterizing equality in (AF) is still unsolved, though progress has been made during the last five years by R. Schneider ([10], [11], [12]),E. Tondorf, and the author ([5], [6], [7]. The method we have introduced hereby in [5] has meanwhile turned out to be applicable to a short and relatively elementary proof of (AF); we present it in this note. We are hopeful it will also contributed to a better understanding of (AF) and open problems connected with the inequality.
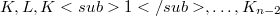 be convex bodies in
be convex bodies in 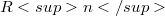 , and let
, and let 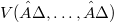 denote mixed volume. Then (AF) (Error rendering LaTeX formula) (For proofs see also Busemann [4], and Leichtweiss [9]). New interest in (AF)has been stimulated recently, partly by the discovery of its equivalence with the Hodge inequality in case of compact projective toric varieties (see Teissier [13], Khovanskij in Burago-Zalgaller [3]).The problem of characterizing equality in (AF) is still unsolved, though progress has been made during the last five years by R. Schneider ([10], [11], [12]),E. Tondorf, and the author ([5], [6], [7]. The method we have introduced hereby in [5] has meanwhile turned out to be applicable to a short and relatively elementary proof of (AF); we present it in this note. We are hopeful it will also contributed to a better understanding of (AF) and open problems connected with the inequality.
denote mixed volume. Then (AF) (Error rendering LaTeX formula) (For proofs see also Busemann [4], and Leichtweiss [9]). New interest in (AF)has been stimulated recently, partly by the discovery of its equivalence with the Hodge inequality in case of compact projective toric varieties (see Teissier [13], Khovanskij in Burago-Zalgaller [3]).The problem of characterizing equality in (AF) is still unsolved, though progress has been made during the last five years by R. Schneider ([10], [11], [12]),E. Tondorf, and the author ([5], [6], [7]. The method we have introduced hereby in [5] has meanwhile turned out to be applicable to a short and relatively elementary proof of (AF); we present it in this note. We are hopeful it will also contributed to a better understanding of (AF) and open problems connected with the inequality.DOI Code:
10.1285/i15900932v10supn1p243
Full Text: PDF


