The first Chern class of Riemannian 3-symmetric spaces: the classical case
Abstract
The existence of Einstein metrics compatible with J on a compact connected almost complex manifold 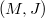 is deeply concerned with its characteristic classes.Using the method of A. Borel and F. Hirzebruch,we prove that an irreducible simply connected (non-Kähler) compact Riemannian 3-symmetric space
is deeply concerned with its characteristic classes.Using the method of A. Borel and F. Hirzebruch,we prove that an irreducible simply connected (non-Kähler) compact Riemannian 3-symmetric space 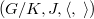 is Einstein if and only if the first Chern class of
is Einstein if and only if the first Chern class of 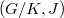 vanishes.
vanishes.
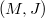 is deeply concerned with its characteristic classes.Using the method of A. Borel and F. Hirzebruch,we prove that an irreducible simply connected (non-Kähler) compact Riemannian 3-symmetric space
is deeply concerned with its characteristic classes.Using the method of A. Borel and F. Hirzebruch,we prove that an irreducible simply connected (non-Kähler) compact Riemannian 3-symmetric space 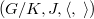 is Einstein if and only if the first Chern class of
is Einstein if and only if the first Chern class of 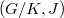 vanishes.
vanishes.DOI Code:
10.1285/i15900932v10n1p141
Full Text: PDF


