Note on planar functions over the reals
Abstract
The following construction was used in a paper of Kárteszi [7] illustrating the role of Cremona transformations for secondary school students.This is a typical construction in the theory of flat affine planes, see Salzmann [9], Groh [4] and due to Dembowski and Ostrom [3] for the case of finite ground fields. Let 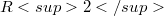 be the classical euclidean affine plane and
be the classical euclidean affine plane and 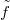 be the graph of a real function
be the graph of a real function 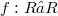 (R denotes the field of real numbers).Define a new incidence structure
(R denotes the field of real numbers).Define a new incidence structure 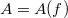 on the points of
on the points of 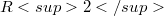 in which the new lines are the vertical lines of
in which the new lines are the vertical lines of 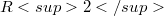 and the translates of
and the translates of 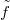 .The incidence is the set-theoretical element of relation. (For the definition of incidence structure,affine plane etc. we refer to Dembowski [2]).
.The incidence is the set-theoretical element of relation. (For the definition of incidence structure,affine plane etc. we refer to Dembowski [2]).
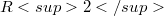 be the classical euclidean affine plane and
be the classical euclidean affine plane and 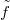 be the graph of a real function
be the graph of a real function 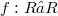 (R denotes the field of real numbers).Define a new incidence structure
(R denotes the field of real numbers).Define a new incidence structure 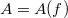 on the points of
on the points of 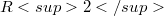 in which the new lines are the vertical lines of
in which the new lines are the vertical lines of 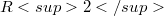 and the translates of
and the translates of 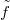 .The incidence is the set-theoretical element of relation. (For the definition of incidence structure,affine plane etc. we refer to Dembowski [2]).
.The incidence is the set-theoretical element of relation. (For the definition of incidence structure,affine plane etc. we refer to Dembowski [2]).DOI Code:
10.1285/i15900932v10n1p59
Full Text: PDF


