On Banach algebras with a Jordan involution
Abstract
Let A be a Banach algebra. By a Jordan involution 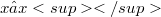 on A we mean a conjugate-linear mapping of A onto A where
on A we mean a conjugate-linear mapping of A onto A where 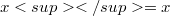 for all x in A and (Error rendering LaTeX formula) for all
for all x in A and (Error rendering LaTeX formula) for all 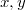 in A. Of course any involution is automatically a Jordan involution. An easy example of a Jordan involution which is not an involution is given, for the algebra of all complex two-by-two matrices, by $$≤ft(\begin{array}{cc} a & b \\
c & d \\
\end{array}\right)#= ≤ft(
\begin{array}{cc}
\bar{a} & \bar{b }\\
\bar{c} & \bar{d} \\
\end{array}\right)$$
In this note we provide one instance where a Jordan involution is compelled to be an involution. Say
in A. Of course any involution is automatically a Jordan involution. An easy example of a Jordan involution which is not an involution is given, for the algebra of all complex two-by-two matrices, by $$≤ft(\begin{array}{cc} a & b \\
c & d \\
\end{array}\right)#= ≤ft(
\begin{array}{cc}
\bar{a} & \bar{b }\\
\bar{c} & \bar{d} \\
\end{array}\right)$$
In this note we provide one instance where a Jordan involution is compelled to be an involution. Say 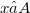 is
is  -normal if x permutes with
-normal if x permutes with 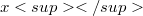 and
and  -self-adjoint if
-self-adjoint if 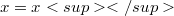 . Let y be
. Let y be  -normal. Then (Error rendering LaTeX formula) so that
-normal. Then (Error rendering LaTeX formula) so that 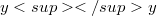 is
is  -self-adjoint. By [5, pp. 481-2]we know that
(Error rendering LaTeX formula) for all
-self-adjoint. By [5, pp. 481-2]we know that
(Error rendering LaTeX formula) for all 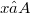 and all positive integers n. Also
and all positive integers n. Also 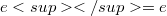 if A has an identity e.
if A has an identity e.
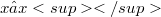 on A we mean a conjugate-linear mapping of A onto A where
on A we mean a conjugate-linear mapping of A onto A where 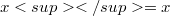 for all x in A and (Error rendering LaTeX formula) for all
for all x in A and (Error rendering LaTeX formula) for all 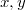 in A. Of course any involution is automatically a Jordan involution. An easy example of a Jordan involution which is not an involution is given, for the algebra of all complex two-by-two matrices, by $$≤ft(\begin{array}{cc} a & b \\
c & d \\
\end{array}\right)#= ≤ft(
\begin{array}{cc}
\bar{a} & \bar{b }\\
\bar{c} & \bar{d} \\
\end{array}\right)$$
In this note we provide one instance where a Jordan involution is compelled to be an involution. Say
in A. Of course any involution is automatically a Jordan involution. An easy example of a Jordan involution which is not an involution is given, for the algebra of all complex two-by-two matrices, by $$≤ft(\begin{array}{cc} a & b \\
c & d \\
\end{array}\right)#= ≤ft(
\begin{array}{cc}
\bar{a} & \bar{b }\\
\bar{c} & \bar{d} \\
\end{array}\right)$$
In this note we provide one instance where a Jordan involution is compelled to be an involution. Say 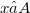 is
is  -normal if x permutes with
-normal if x permutes with 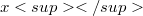 and
and  -self-adjoint if
-self-adjoint if 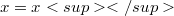 . Let y be
. Let y be  -normal. Then (Error rendering LaTeX formula) so that
-normal. Then (Error rendering LaTeX formula) so that 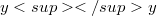 is
is  -self-adjoint. By [5, pp. 481-2]we know that
(Error rendering LaTeX formula) for all
-self-adjoint. By [5, pp. 481-2]we know that
(Error rendering LaTeX formula) for all 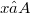 and all positive integers n. Also
and all positive integers n. Also 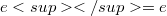 if A has an identity e.
if A has an identity e.DOI Code:
10.1285/i15900932v11p331
Full Text: PDF


