A remark on bases in quotients of 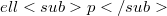 when
when 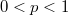
Abstract
In [9] Stiles showed that if 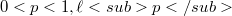 has an infinite-dimensional closed subspace which contains no complemented copy of
has an infinite-dimensional closed subspace which contains no complemented copy of 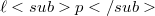 ; this contrasts with the well-known result of Pelczynski [5] for
; this contrasts with the well-known result of Pelczynski [5] for 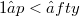 . The following curious theorem is the main result of this note: Theorem 1. Let M be an infinite-dimensional closed subspace of
. The following curious theorem is the main result of this note: Theorem 1. Let M be an infinite-dimensional closed subspace of 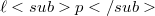 where
where 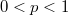 . Suppose
. Suppose 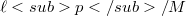 has a basis. Then M contains a subspace isomorphic to
has a basis. Then M contains a subspace isomorphic to 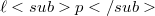 and complemented in
and complemented in 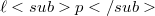 .
.
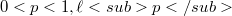 has an infinite-dimensional closed subspace which contains no complemented copy of
has an infinite-dimensional closed subspace which contains no complemented copy of 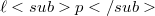 ; this contrasts with the well-known result of Pelczynski [5] for
; this contrasts with the well-known result of Pelczynski [5] for 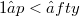 . The following curious theorem is the main result of this note: Theorem 1. Let M be an infinite-dimensional closed subspace of
. The following curious theorem is the main result of this note: Theorem 1. Let M be an infinite-dimensional closed subspace of 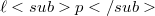 where
where 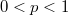 . Suppose
. Suppose 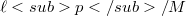 has a basis. Then M contains a subspace isomorphic to
has a basis. Then M contains a subspace isomorphic to 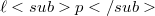 and complemented in
and complemented in 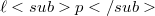 .
.DOI Code:
10.1285/i15900932v11p231
Full Text: PDF


