Convergence of finite multistep predictors from incorrect models and its role in model selection
Abstract
In a recent paper [5],we described a generalization to univariate time series models of the hypothesis testing procedure of Vuong [13] for comparing incorrect statistical models for independent data. The focus of [5] was on model selection criteria related to one-step-ahead forecasting performance. We suggested there that when p-step-ahead prediction is the goal, with 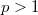 ,then different test statistics should be used for each choice of p. To identify appropriate test statistics and determine their aymptotic distribution, information is needed about the rate at which predictors based on n observations converge as
,then different test statistics should be used for each choice of p. To identify appropriate test statistics and determine their aymptotic distribution, information is needed about the rate at which predictors based on n observations converge as 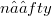 .This note provides some of the needed convergence and dstributional results, also for the case of r-dimensional vector time series. Our approach rests on generalizations of the finite-section inequality and related convergence results of Baxter [1], [2] for one-step-ahead predictors of scalar time series. To make our results accessible to a larger circle of readers, we will not formulate them in the Banach algebra framework utilized by Hirschman [9], but it will be clear to the mathematical reader that this level of generality is attainable and natural.
.This note provides some of the needed convergence and dstributional results, also for the case of r-dimensional vector time series. Our approach rests on generalizations of the finite-section inequality and related convergence results of Baxter [1], [2] for one-step-ahead predictors of scalar time series. To make our results accessible to a larger circle of readers, we will not formulate them in the Banach algebra framework utilized by Hirschman [9], but it will be clear to the mathematical reader that this level of generality is attainable and natural.
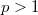 ,then different test statistics should be used for each choice of p. To identify appropriate test statistics and determine their aymptotic distribution, information is needed about the rate at which predictors based on n observations converge as
,then different test statistics should be used for each choice of p. To identify appropriate test statistics and determine their aymptotic distribution, information is needed about the rate at which predictors based on n observations converge as 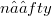 .This note provides some of the needed convergence and dstributional results, also for the case of r-dimensional vector time series. Our approach rests on generalizations of the finite-section inequality and related convergence results of Baxter [1], [2] for one-step-ahead predictors of scalar time series. To make our results accessible to a larger circle of readers, we will not formulate them in the Banach algebra framework utilized by Hirschman [9], but it will be clear to the mathematical reader that this level of generality is attainable and natural.
.This note provides some of the needed convergence and dstributional results, also for the case of r-dimensional vector time series. Our approach rests on generalizations of the finite-section inequality and related convergence results of Baxter [1], [2] for one-step-ahead predictors of scalar time series. To make our results accessible to a larger circle of readers, we will not formulate them in the Banach algebra framework utilized by Hirschman [9], but it will be clear to the mathematical reader that this level of generality is attainable and natural.DOI Code:
10.1285/i15900932v11p145
Full Text: PDF


