An application of spectral calculus to the problem of saturation in approximation theory
Abstract
Let 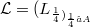 , be a net of bounded linear operators on the Banach space E converging strongly to the identity on E. For a given complex-valued function f of a fixed type we consider the net
, be a net of bounded linear operators on the Banach space E converging strongly to the identity on E. For a given complex-valued function f of a fixed type we consider the net 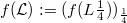 . Among other things we shall show that under reasonable conditions the saturation space of with respect to a given net
. Among other things we shall show that under reasonable conditions the saturation space of with respect to a given net 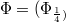 of positive real numbers converging to zero is equal to that one of
of positive real numbers converging to zero is equal to that one of 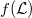 . More generally we consider nets
. More generally we consider nets 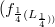 where
where 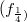 is a net of complex-valued functions and we determine the saturation space of such a net in dependence of the saturation space of .
is a net of complex-valued functions and we determine the saturation space of such a net in dependence of the saturation space of .
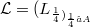 , be a net of bounded linear operators on the Banach space E converging strongly to the identity on E. For a given complex-valued function f of a fixed type we consider the net
, be a net of bounded linear operators on the Banach space E converging strongly to the identity on E. For a given complex-valued function f of a fixed type we consider the net 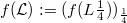 . Among other things we shall show that under reasonable conditions the saturation space of with respect to a given net
. Among other things we shall show that under reasonable conditions the saturation space of with respect to a given net 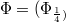 of positive real numbers converging to zero is equal to that one of
of positive real numbers converging to zero is equal to that one of 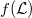 . More generally we consider nets
. More generally we consider nets 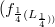 where
where 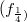 is a net of complex-valued functions and we determine the saturation space of such a net in dependence of the saturation space of .
is a net of complex-valued functions and we determine the saturation space of such a net in dependence of the saturation space of .DOI Code:
10.1285/i15900932v12p291
Full Text: PDF


