Amaximal extension of Kothe\'s homomorphism theorem
Abstract
In 1958, Prof. T.Kato gave the following perturbation theorem: Let 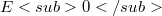 , and
, and 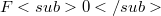 be subspaces of Banach spaces E and F, respectively, and let
be subspaces of Banach spaces E and F, respectively, and let 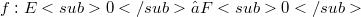 be a linear surjective map from
be a linear surjective map from 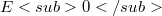 onto
onto 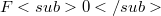 with closed graph in
with closed graph in 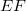 .If
.If 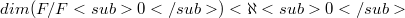 , then f is open and
, then f is open and 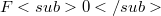 is closed in F [4]. Ten years later, Prof Dr. G. Köthe gave two generalizations [5] which enhanced and were enhanced by considerations of codimension [7], Baire-like (BL) spaces [11a], and quasi-Baire (QB) spaces [11a, 9], and thus, together with a Robertson-Robertson Closed Graph Theorem (cf. [14]), provided significant external impetus for the early study of strong barelledness conditions. Viewed as yet another version of the Kato result, Köthe's Homomorphism Theorem replaces «Banach spaces» with the more general «(LF)-spaces» (cf. 8.4.13 of [6]). Here, again, strong barelledness [12] kindly repays Köthe and allows us to replace «< \aleph_0» with «< c ». This is, easily, the best possible extension as regards codimension of
is closed in F [4]. Ten years later, Prof Dr. G. Köthe gave two generalizations [5] which enhanced and were enhanced by considerations of codimension [7], Baire-like (BL) spaces [11a], and quasi-Baire (QB) spaces [11a, 9], and thus, together with a Robertson-Robertson Closed Graph Theorem (cf. [14]), provided significant external impetus for the early study of strong barelledness conditions. Viewed as yet another version of the Kato result, Köthe's Homomorphism Theorem replaces «Banach spaces» with the more general «(LF)-spaces» (cf. 8.4.13 of [6]). Here, again, strong barelledness [12] kindly repays Köthe and allows us to replace «< \aleph_0» with «< c ». This is, easily, the best possible extension as regards codimension of 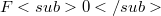 .
.
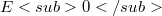 , and
, and 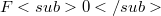 be subspaces of Banach spaces E and F, respectively, and let
be subspaces of Banach spaces E and F, respectively, and let 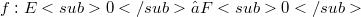 be a linear surjective map from
be a linear surjective map from 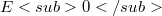 onto
onto 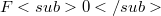 with closed graph in
with closed graph in 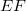 .If
.If 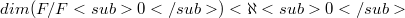 , then f is open and
, then f is open and 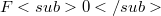 is closed in F [4]. Ten years later, Prof Dr. G. Köthe gave two generalizations [5] which enhanced and were enhanced by considerations of codimension [7], Baire-like (BL) spaces [11a], and quasi-Baire (QB) spaces [11a, 9], and thus, together with a Robertson-Robertson Closed Graph Theorem (cf. [14]), provided significant external impetus for the early study of strong barelledness conditions. Viewed as yet another version of the Kato result, Köthe's Homomorphism Theorem replaces «Banach spaces» with the more general «(LF)-spaces» (cf. 8.4.13 of [6]). Here, again, strong barelledness [12] kindly repays Köthe and allows us to replace «< \aleph_0» with «< c ». This is, easily, the best possible extension as regards codimension of
is closed in F [4]. Ten years later, Prof Dr. G. Köthe gave two generalizations [5] which enhanced and were enhanced by considerations of codimension [7], Baire-like (BL) spaces [11a], and quasi-Baire (QB) spaces [11a, 9], and thus, together with a Robertson-Robertson Closed Graph Theorem (cf. [14]), provided significant external impetus for the early study of strong barelledness conditions. Viewed as yet another version of the Kato result, Köthe's Homomorphism Theorem replaces «Banach spaces» with the more general «(LF)-spaces» (cf. 8.4.13 of [6]). Here, again, strong barelledness [12] kindly repays Köthe and allows us to replace «< \aleph_0» with «< c ». This is, easily, the best possible extension as regards codimension of 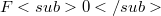 .
.DOI Code:
10.1285/i15900932v12p229
Full Text: PDF


