Vector space partitions and designs Part II – constructions
Abstract
This article is the second part and companion article to Part I on the basictheory of what are called focal-spreads; partitions of finite vector spacesof dimension 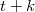 by one subspace of dimension
by one subspace of dimension 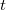 (the `focus') and theremaining subspaces of dimension
(the `focus') and theremaining subspaces of dimension 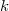 , a `focal-spread of type
, a `focal-spread of type 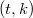 '
' InPart I, additive focal-spreads are shown to be equivalent to additivepartial spreads. Focal-spreads of type
InPart I, additive focal-spreads are shown to be equivalent to additivepartial spreads. Focal-spreads of type 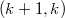 also produce
also produce  -designs, \ and various other double and triple-spreads.Also, in Part I, there are two different methods given to constructfocal-spreads, one of which is due to Beutelspacher, the other method beinga coordinate method similar to the theory available for translation planes.Here, we shall give a new construction that we term "going up," which alsoallows a specification of certain subplanes of the focal-spread.
-designs, \ and various other double and triple-spreads.Also, in Part I, there are two different methods given to constructfocal-spreads, one of which is due to Beutelspacher, the other method beinga coordinate method similar to the theory available for translation planes.Here, we shall give a new construction that we term "going up," which alsoallows a specification of certain subplanes of the focal-spread.
Full Text: PDF


