On homotopy Lie algebra structures in the rings of differential operators
Abstract
We study the Schlessinger-Stasheff's homotopy Lie structures on the associative algebras of differential operators Diff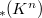 w.r.t. n independent variables.The Wronskians are proved to provide the relations for the generators of these algebras; two remarkable identities for the Wronskian and the Vandermonde determinants are obtained. We axiomize the idea of the Hochschild cohomologies and extend the group
w.r.t. n independent variables.The Wronskians are proved to provide the relations for the generators of these algebras; two remarkable identities for the Wronskian and the Vandermonde determinants are obtained. We axiomize the idea of the Hochschild cohomologies and extend the group 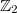 of signs
of signs 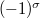 to the circumpherence
to the circumpherence 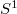 . Then, the concept of associative homotopy Lie algebras admits nontrivial generalizations.
. Then, the concept of associative homotopy Lie algebras admits nontrivial generalizations.
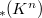 w.r.t. n independent variables.The Wronskians are proved to provide the relations for the generators of these algebras; two remarkable identities for the Wronskian and the Vandermonde determinants are obtained. We axiomize the idea of the Hochschild cohomologies and extend the group
w.r.t. n independent variables.The Wronskians are proved to provide the relations for the generators of these algebras; two remarkable identities for the Wronskian and the Vandermonde determinants are obtained. We axiomize the idea of the Hochschild cohomologies and extend the group 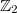 of signs
of signs 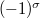 to the circumpherence
to the circumpherence 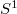 . Then, the concept of associative homotopy Lie algebras admits nontrivial generalizations.
. Then, the concept of associative homotopy Lie algebras admits nontrivial generalizations.DOI Code:
10.1285/i15900932v23n1p83
Keywords:
SH algebras; Differential operators; Wronskian determinants; CFT
Classification:
81T40; 15A15; 17B66; 15A54; 15A90; 17B68; 53C21
Full Text: PDF


