On The Maximum Jump Number 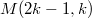
Abstract
If 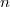 and
and 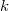 (
(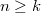 ) are large enough , it is quite difficult to give the value of
) are large enough , it is quite difficult to give the value of 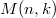 . R.A. Brualdi and H.C. Jung gave a table about the value of
. R.A. Brualdi and H.C. Jung gave a table about the value of 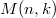 for
for 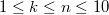 . In this paper, we show that
. In this paper, we show that 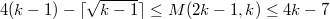 holds for
holds for 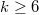 . Hence,
. Hence, 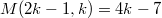 holds for
holds for 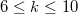 , which verifies that their conjecture
, which verifies that their conjecture 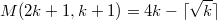 holds for
holds for 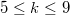 , and disprove their conjecture
, and disprove their conjecture 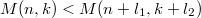 for
for 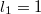 ,
, 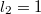 .
.
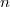 and
and 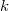 (
(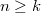 ) are large enough , it is quite difficult to give the value of
) are large enough , it is quite difficult to give the value of 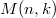 . R.A. Brualdi and H.C. Jung gave a table about the value of
. R.A. Brualdi and H.C. Jung gave a table about the value of 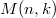 for
for 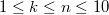 . In this paper, we show that
. In this paper, we show that 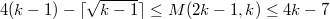 holds for
holds for 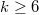 . Hence,
. Hence, 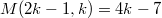 holds for
holds for 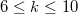 , which verifies that their conjecture
, which verifies that their conjecture 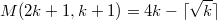 holds for
holds for 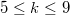 , and disprove their conjecture
, and disprove their conjecture 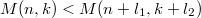 for
for 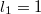 ,
, 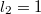 .
.DOI Code:
10.1285/i15900932v23n1p71
Keywords:
(0,1)-matrices; Jump number; Stair number; Conjecture
Classification:
05B20; 15A36
Full Text: PDF


