On the number of 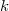 -gons in finite projective planes
-gons in finite projective planes
Abstract
Let 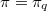 denote a finite projective plane of order
denote a finite projective plane of order 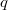 , and let
, and let 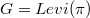 be the bipartite point-line incidence graph of
be the bipartite point-line incidence graph of 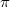 . For
. For 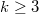 , let
, let 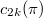 denote the number of cycles of length
denote the number of cycles of length 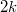 in
in  . Are the numbers
. Are the numbers 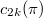 the same for all
the same for all 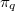 ? We prove that this is the case for
? We prove that this is the case for 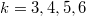 by computing these numbers.
by computing these numbers.
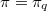 denote a finite projective plane of order
denote a finite projective plane of order 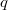 , and let
, and let 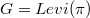 be the bipartite point-line incidence graph of
be the bipartite point-line incidence graph of 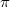 . For
. For 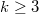 , let
, let 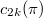 denote the number of cycles of length
denote the number of cycles of length 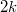 in
in  . Are the numbers
. Are the numbers 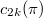 the same for all
the same for all 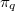 ? We prove that this is the case for
? We prove that this is the case for 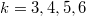 by computing these numbers.
by computing these numbers.DOI Code:
10.1285/i15900932v29n1supplp135
Keywords:
Projective planes; embeddings; k-cycles; Levi graphs
Projective planes; embeddings; k-cycles; Levi graphs
Full Text: PDF


