Latin Squares, Homologies and Eulerӳ Conjecture
Abstract
We construct pairs of orthogonal Latin Squares of order  by means of suitable orthomorphisms of the cyclic group of order
by means of suitable orthomorphisms of the cyclic group of order 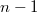 . These pairs always have
. These pairs always have 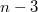 confluent common transversals. They lead to partial planes of order
confluent common transversals. They lead to partial planes of order  with
with 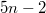 lines and
lines and 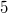 complete points. Also, we provide an easy construction of counter examples to Euler's conjecture.
complete points. Also, we provide an easy construction of counter examples to Euler's conjecture.
 by means of suitable orthomorphisms of the cyclic group of order
by means of suitable orthomorphisms of the cyclic group of order 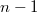 . These pairs always have
. These pairs always have 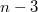 confluent common transversals. They lead to partial planes of order
confluent common transversals. They lead to partial planes of order  with
with 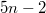 lines and
lines and 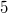 complete points. Also, we provide an easy construction of counter examples to Euler's conjecture.
complete points. Also, we provide an easy construction of counter examples to Euler's conjecture.DOI Code:
10.1285/i15900932v29n1supplp115
Keywords:
Latin Squares; Orthomorphisms; Projective Planes
Latin Squares; Orthomorphisms; Projective Planes
Full Text: PDF


