On the Multiplicative Structure of Quasifields and Semifields: Cyclic and Acyclic Loops
Abstract
This note is concerned with the multiplicative loop 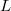 of a finite quasifield or semifield, and the associated geometry. It investigates when the principal powers of some element of the multiplicative loop
of a finite quasifield or semifield, and the associated geometry. It investigates when the principal powers of some element of the multiplicative loop 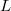 ranges over the whole loop: in this situation the loop
ranges over the whole loop: in this situation the loop 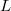 is cyclic (or primitive) and is acyclic otherwise. A conjecture of Wene essentially asserts that a finite semifield cannot be acyclic.No counterexamples to the Wene conjecture are known for semifields of order
is cyclic (or primitive) and is acyclic otherwise. A conjecture of Wene essentially asserts that a finite semifield cannot be acyclic.No counterexamples to the Wene conjecture are known for semifields of order 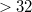 ; in fact, in many situations the Wene conjecture is known to hold, as established in various papersby Wene, Rùa and Hamilton. The primary aim of this note is to show that, in contrast to the above situation,there exists at least one acyclic quasifield for every square prime powerorder
; in fact, in many situations the Wene conjecture is known to hold, as established in various papersby Wene, Rùa and Hamilton. The primary aim of this note is to show that, in contrast to the above situation,there exists at least one acyclic quasifield for every square prime powerorder 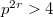 . Additionally, we include a simple conceptual proof ofa theorem of Rùa, that establishes the primitivity ofthree-dimensional semifields.
. Additionally, we include a simple conceptual proof ofa theorem of Rùa, that establishes the primitivity ofthree-dimensional semifields.
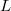 of a finite quasifield or semifield, and the associated geometry. It investigates when the principal powers of some element of the multiplicative loop
of a finite quasifield or semifield, and the associated geometry. It investigates when the principal powers of some element of the multiplicative loop 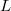 ranges over the whole loop: in this situation the loop
ranges over the whole loop: in this situation the loop 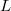 is cyclic (or primitive) and is acyclic otherwise. A conjecture of Wene essentially asserts that a finite semifield cannot be acyclic.No counterexamples to the Wene conjecture are known for semifields of order
is cyclic (or primitive) and is acyclic otherwise. A conjecture of Wene essentially asserts that a finite semifield cannot be acyclic.No counterexamples to the Wene conjecture are known for semifields of order 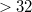 ; in fact, in many situations the Wene conjecture is known to hold, as established in various papersby Wene, Rùa and Hamilton. The primary aim of this note is to show that, in contrast to the above situation,there exists at least one acyclic quasifield for every square prime powerorder
; in fact, in many situations the Wene conjecture is known to hold, as established in various papersby Wene, Rùa and Hamilton. The primary aim of this note is to show that, in contrast to the above situation,there exists at least one acyclic quasifield for every square prime powerorder 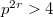 . Additionally, we include a simple conceptual proof ofa theorem of Rùa, that establishes the primitivity ofthree-dimensional semifields.
. Additionally, we include a simple conceptual proof ofa theorem of Rùa, that establishes the primitivity ofthree-dimensional semifields.DOI Code:
10.1285/i15900932v29n1supplp45
Keywords:
loops; quasifields; semifields; derivation
loops; quasifields; semifields; derivation
Full Text: PDF


