Some partitions in Figueroa planes
Abstract
Using Grundhöfer's construction of the Figueroa planes from Pappian planes which have an order 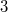 planar collineation
planar collineation 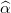 , we show that any Figueroa plane (finite or infinite) has a partition of the complement of any proper (
, we show that any Figueroa plane (finite or infinite) has a partition of the complement of any proper (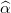 )-invariant triangle mostly into subplanes together with a few collinear point sets (from the point set view) and a few concurrent line sets (from the line set view). The partition shows that each Figueroa line (regarded as a set of points) is either the same as a Pappian line or consists mostly of a disjoint union of subplanes of the Pappian plane (most lines are of this latter type) anddually. This last sentence is true with "Figueroa" and "Pappian" interchanged. There are many collinear subsets of Figueroa points which are a subset of the set of points of a Pappian conic and dually.
)-invariant triangle mostly into subplanes together with a few collinear point sets (from the point set view) and a few concurrent line sets (from the line set view). The partition shows that each Figueroa line (regarded as a set of points) is either the same as a Pappian line or consists mostly of a disjoint union of subplanes of the Pappian plane (most lines are of this latter type) anddually. This last sentence is true with "Figueroa" and "Pappian" interchanged. There are many collinear subsets of Figueroa points which are a subset of the set of points of a Pappian conic and dually.
projective plane; Figueroa plane; Pappian plane; subplane; partition; conic; oval; hyperoval
Full Text: PDF


