Table Of Contents
| Introduzione | |
| E. Barone | 1-2 |
| Premesse e definizioni | |
| E. Barone | 3-6 |
| Omomorfismi, isomorfismi | |
| E. Barone | 7-9 |
| Ideali e filtri massimali (o ultrafiltri) | |
| E. Barone | 8-9 |
| Legame con gli anelli algebrici | |
| E. Barone | 9-10 |
| Campi d'insiemi ridotti e perfetti | |
| E. Barone | 10-16 |
| Il teorema di rappresentazione di Stone (1934-1938) | |
| E. Barone | 16-22 |
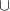 e e 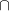 infinite in un'algebra Booleana A infinite in un'algebra Booleana A |
|
| E. Barone | 22-25 |
| Algebre Booleane m-complete | |
| E. Barone | 26-29 |
| m-ideali, m-filtri. Algebre quozienti | |
| E. Barone | 29-36 |
| m-omomorfismi, atomi, ed interpretazione negli spazi di Stone | |
| E. Barone | 36-39 |
| Applicazioni alla teoria della misura | |
| E. Barone | 39-51 |
| Bibliografia | |
| E. Barone | 52-52 |
| Indice | |
| E. Barone |

This work is licensed under a Creative Commons Attribuzione - Non commerciale - Non opere derivate 3.0 Italia License.


