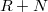|
V.
Manco
,
G.
Metafune
,
C.
Spina
|
Full Version (PDF)
|

ISBN: 88-8305-031-2
e-ISBN: 88-8305-032-0
Questo quaderno è basato sulle lezioni tenute da G. Metafune nel corso di Analisi Reale ed Equazioni Ellittiche; è la naturale continuazione del quaderno 4/2004, ma può essere letto indipendentemente.
La trattazione è divisa in due parti. Nella prima vengono trattati i teoremi classici di interpolazione di Riesz-Thorin e Marcinkiewicz cercando di mostrare una varietà di applicazioni anche al di fuori della teoria delle equazioni ellittiche.
La seconda parte inizia con la disuguaglianza di Calderòn-Zygmund che permette di stimare le derivate seconde di una funzione in W2,p(RN) (1 < p < ∞) col suo Laplaciano.Una volta ottenuto questo risultato, gli usuali metodi di perturbazione, localizzazione e congelamento dei coefficienti permettono di ottenere le stime a priori Lp per un operatore ellittico generale. La risolubilità del problema ellittico per il Laplaciano, le stime a priori e il metodo di continuità consentono poi di avere teoremi di esistenza e unicità.
Table Of Contents
| Introduzione |
PDF
|
|
V.
Manco
,
G.
Metafune
,
C.
Spina
|
|
| Alcuni teoremi classici di interpolazione |
PDF
|
|
V.
Manco
,
G.
Metafune
,
C.
Spina
|
1-39 |
| L'equazione di Poisson |
PDF
|
|
V.
Manco
,
G.
Metafune
,
C.
Spina
|
41-59 |
Operatori ellettici in 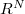 |
PDF
|
|
V. Manco, G. Metafune, C. Spina |
61-74 |
Operatori ellittici in 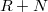 |
PDF
|
|
V. Manco, G. Metafune, C. Spina |
75-82 |
| Operatori ellittici in domini limitati |
PDF
|
|
V.
Manco
,
G.
Metafune
,
C.
Spina
|
83-93 |
| Regolarità di ordine superiore |
PDF
|
|
V.
Manco
,
G.
Metafune
,
C.
Spina
|
95-101 |
Questo sito utilizza un cookie tecnico per consentire la corretta navigazione. Se vuoi saperne di più consulta l'
informativa estesa.
 This work is licensed under a Creative Commons Attribuzione - Non commerciale - Non opere derivate 3.0 Italia License.
This work is licensed under a Creative Commons Attribuzione - Non commerciale - Non opere derivate 3.0 Italia License.
 ISBN: 88-8305-031-2
ISBN: 88-8305-031-2