Introduzione
Abstract
It
In questo lavoro si studia il problema di valori al contorno (1)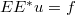 (2)
(2) 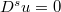 su
su 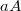 per
per 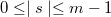 dove
dove 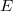 è un particolare operatore ellitico di ordine
è un particolare operatore ellitico di ordine 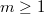 e
e 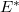 è l'operatore formalmente aggiunto di
è l'operatore formalmente aggiunto di 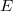 . Di tali operatori è possibile costuire gli operatori soluzioni fondamentali. Ciò permette di dimostrare l'esistenza e l'unicità della soluzione del problema (1),(2) in una opportuna classe
. Di tali operatori è possibile costuire gli operatori soluzioni fondamentali. Ciò permette di dimostrare l'esistenza e l'unicità della soluzione del problema (1),(2) in una opportuna classe 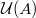 per ogni
per ogni 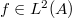 . Il fatto più saliente è che dell'operatore di Green del problema (1),(2) si dà la forma esplicita. Ciò permette di studiare il problema di autovalori relativo ad (1),(2) usando (oltre che il metodo di Rayleigh-Ritz) quello degli invarianti ortogonali.
. Il fatto più saliente è che dell'operatore di Green del problema (1),(2) si dà la forma esplicita. Ciò permette di studiare il problema di autovalori relativo ad (1),(2) usando (oltre che il metodo di Rayleigh-Ritz) quello degli invarianti ortogonali.
In questo lavoro si studia il problema di valori al contorno (1)
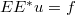 (2)
(2) 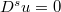 su
su 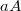 per
per 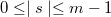 dove
dove 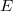 è un particolare operatore ellitico di ordine
è un particolare operatore ellitico di ordine 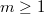 e
e 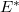 è l'operatore formalmente aggiunto di
è l'operatore formalmente aggiunto di 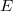 . Di tali operatori è possibile costuire gli operatori soluzioni fondamentali. Ciò permette di dimostrare l'esistenza e l'unicità della soluzione del problema (1),(2) in una opportuna classe
. Di tali operatori è possibile costuire gli operatori soluzioni fondamentali. Ciò permette di dimostrare l'esistenza e l'unicità della soluzione del problema (1),(2) in una opportuna classe 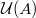 per ogni
per ogni 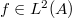 . Il fatto più saliente è che dell'operatore di Green del problema (1),(2) si dà la forma esplicita. Ciò permette di studiare il problema di autovalori relativo ad (1),(2) usando (oltre che il metodo di Rayleigh-Ritz) quello degli invarianti ortogonali.
. Il fatto più saliente è che dell'operatore di Green del problema (1),(2) si dà la forma esplicita. Ciò permette di studiare il problema di autovalori relativo ad (1),(2) usando (oltre che il metodo di Rayleigh-Ritz) quello degli invarianti ortogonali.DOI Code:
§
Full Text: PDF


