Introduction
Abstract
It
In questo lavoro noi dimostriamo che in una struttura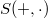 introdotta di J. Szép, dove
introdotta di J. Szép, dove 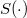 è un gruppo finito,
è un gruppo finito, 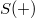 un semigruppo e sussistono certe proprietà distributive,(vedi (1) e (2) con
un semigruppo e sussistono certe proprietà distributive,(vedi (1) e (2) con 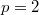 oppure
oppure 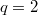 , il gruppo
, il gruppo 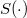 è necessariamente prodotto diretto di gruppi di ordine 3. Inoltre proviamo che
è necessariamente prodotto diretto di gruppi di ordine 3. Inoltre proviamo che 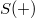 è anch'esso necessariamente un gruppo per il quale esiste
è anch'esso necessariamente un gruppo per il quale esiste 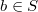 tale che per ogni
tale che per ogni 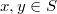 risulta
risulta 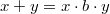 .
.
In questo lavoro noi dimostriamo che in una struttura
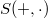 introdotta di J. Szép, dove
introdotta di J. Szép, dove 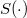 è un gruppo finito,
è un gruppo finito, 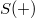 un semigruppo e sussistono certe proprietà distributive,(vedi (1) e (2) con
un semigruppo e sussistono certe proprietà distributive,(vedi (1) e (2) con 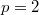 oppure
oppure 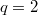 , il gruppo
, il gruppo 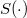 è necessariamente prodotto diretto di gruppi di ordine 3. Inoltre proviamo che
è necessariamente prodotto diretto di gruppi di ordine 3. Inoltre proviamo che 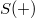 è anch'esso necessariamente un gruppo per il quale esiste
è anch'esso necessariamente un gruppo per il quale esiste 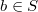 tale che per ogni
tale che per ogni 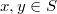 risulta
risulta 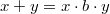 .
.DOI Code:
§
Full Text: PDF


