Semigruppi di Markov ed operatori differenziali
Abstract
It
In questo capitolo introduciamo la nozione di semigruppo di Markov in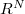 e proviamo che ad ogni operatore differenziale lineare ellittico del secondo ordine a coefficienti illimitati in
e proviamo che ad ogni operatore differenziale lineare ellittico del secondo ordine a coefficienti illimitati in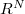 , A, è possibile associare un siffatto semigruppo,
, A, è possibile associare un siffatto semigruppo, 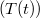 . Per far ciò, ricorriamo essenzialmente ad un argomento di localizzazione e all'uso delle stime di Schauder locali classiche. Inoltre, discutiamo altre proprietà del semigruppo costruito, tra cui l'irriducibilità e la condizione di strong Feller. Infne, introduciamo la nozione di generatore debole per
. Per far ciò, ricorriamo essenzialmente ad un argomento di localizzazione e all'uso delle stime di Schauder locali classiche. Inoltre, discutiamo altre proprietà del semigruppo costruito, tra cui l'irriducibilità e la condizione di strong Feller. Infne, introduciamo la nozione di generatore debole per 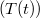 (che non è fortemente continuo, in generale) e ne studiamo la relazione con l'operatore A di partenza.
(che non è fortemente continuo, in generale) e ne studiamo la relazione con l'operatore A di partenza.
In questo capitolo introduciamo la nozione di semigruppo di Markov in
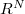 e proviamo che ad ogni operatore differenziale lineare ellittico del secondo ordine a coefficienti illimitati in
e proviamo che ad ogni operatore differenziale lineare ellittico del secondo ordine a coefficienti illimitati in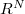 , A, è possibile associare un siffatto semigruppo,
, A, è possibile associare un siffatto semigruppo, 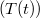 . Per far ciò, ricorriamo essenzialmente ad un argomento di localizzazione e all'uso delle stime di Schauder locali classiche. Inoltre, discutiamo altre proprietà del semigruppo costruito, tra cui l'irriducibilità e la condizione di strong Feller. Infne, introduciamo la nozione di generatore debole per
. Per far ciò, ricorriamo essenzialmente ad un argomento di localizzazione e all'uso delle stime di Schauder locali classiche. Inoltre, discutiamo altre proprietà del semigruppo costruito, tra cui l'irriducibilità e la condizione di strong Feller. Infne, introduciamo la nozione di generatore debole per 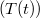 (che non è fortemente continuo, in generale) e ne studiamo la relazione con l'operatore A di partenza.
(che non è fortemente continuo, in generale) e ne studiamo la relazione con l'operatore A di partenza.DOI Code:
§
Full Text: PDF


