Maximal visibility and unions of orthogonally starshaped sets
Abstract
Let S be an orthogonal polygon in the plane. For each point x in S,let 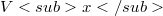 denote the set of points which x sees via staircase paths and let(Error rendering LaTeX formula). For S simply connected, S is starshaped via staircase paths (i.e., orthogonally starshaped) if and only if S contains exactly one such closed set
denote the set of points which x sees via staircase paths and let(Error rendering LaTeX formula). For S simply connected, S is starshaped via staircase paths (i.e., orthogonally starshaped) if and only if S contains exactly one such closed set 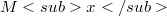 , and when this occurs
, and when this occurs 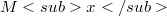 is the staircase kernel of S. In general, if S contains exactly k such distinct closed set
is the staircase kernel of S. In general, if S contains exactly k such distinct closed set 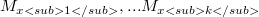 , then S is a union of k (or possibly fewer) orthogonally starshaped sets chosen from
, then S is a union of k (or possibly fewer) orthogonally starshaped sets chosen from 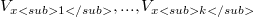 .
.
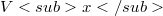 denote the set of points which x sees via staircase paths and let(Error rendering LaTeX formula). For S simply connected, S is starshaped via staircase paths (i.e., orthogonally starshaped) if and only if S contains exactly one such closed set
denote the set of points which x sees via staircase paths and let(Error rendering LaTeX formula). For S simply connected, S is starshaped via staircase paths (i.e., orthogonally starshaped) if and only if S contains exactly one such closed set 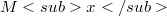 , and when this occurs
, and when this occurs 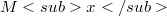 is the staircase kernel of S. In general, if S contains exactly k such distinct closed set
is the staircase kernel of S. In general, if S contains exactly k such distinct closed set 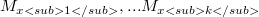 , then S is a union of k (or possibly fewer) orthogonally starshaped sets chosen from
, then S is a union of k (or possibly fewer) orthogonally starshaped sets chosen from 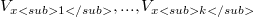 .
.DOI Code:
10.1285/i15900932v24n1p1
Keywords:
Orthogonal polygons; Starshaped via staircase paths
Classification:
52A30
Full Text: PDF


