Finite and locally solvable periodic groups with given intersections of certain subgroups
Abstract
Let G be a group and p be a prime. We say that two subgroups 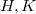 are incident if either
are incident if either 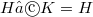 or
or 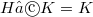 . A group G is an
. A group G is an 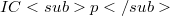 -group if, for any finite non-incident subgroups
-group if, for any finite non-incident subgroups 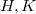 of G, a p-Sylow subgroup of
of G, a p-Sylow subgroup of 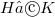 is cyclic.
In this paper we give a complete classification of solvable and locally solvable periodic
is cyclic.
In this paper we give a complete classification of solvable and locally solvable periodic 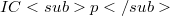 -groups.
-groups.
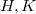 are incident if either
are incident if either 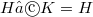 or
or 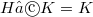 . A group G is an
. A group G is an 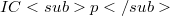 -group if, for any finite non-incident subgroups
-group if, for any finite non-incident subgroups 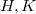 of G, a p-Sylow subgroup of
of G, a p-Sylow subgroup of 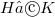 is cyclic.
In this paper we give a complete classification of solvable and locally solvable periodic
is cyclic.
In this paper we give a complete classification of solvable and locally solvable periodic 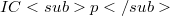 -groups.
-groups.DOI Code:
10.1285/i15900932v14n2p147
Full Text: PDF


