Extending norms on groups
Abstract
Following Farkas, by a norm n on a group G I shall understand a function n on G to the set of non-negative real numbers, satisfying 1. 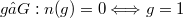 2.
2. 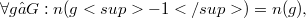 and 3.
and 3. 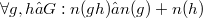 I call n a seminorm, if only
I call n a seminorm, if only 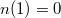 instead of the first condition.
Beginning with some general remarks on normed groups, I will discuss the possibility of extending norms from a normal subgroup to the whole group.A sufficient condition for the existence of such an extension is found, which demands that the inner automorphisms of the whole group do not move the elements of the subgroup too far and that there exists a factor set of the given extension of groups, which is bounded on one side.
So I get a counterpart to the necessary condition, which was found by Farkas in [3].
instead of the first condition.
Beginning with some general remarks on normed groups, I will discuss the possibility of extending norms from a normal subgroup to the whole group.A sufficient condition for the existence of such an extension is found, which demands that the inner automorphisms of the whole group do not move the elements of the subgroup too far and that there exists a factor set of the given extension of groups, which is bounded on one side.
So I get a counterpart to the necessary condition, which was found by Farkas in [3].
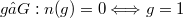 2.
2. 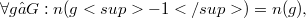 and 3.
and 3. 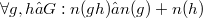 I call n a seminorm, if only
I call n a seminorm, if only 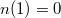 instead of the first condition.
Beginning with some general remarks on normed groups, I will discuss the possibility of extending norms from a normal subgroup to the whole group.A sufficient condition for the existence of such an extension is found, which demands that the inner automorphisms of the whole group do not move the elements of the subgroup too far and that there exists a factor set of the given extension of groups, which is bounded on one side.
So I get a counterpart to the necessary condition, which was found by Farkas in [3].
instead of the first condition.
Beginning with some general remarks on normed groups, I will discuss the possibility of extending norms from a normal subgroup to the whole group.A sufficient condition for the existence of such an extension is found, which demands that the inner automorphisms of the whole group do not move the elements of the subgroup too far and that there exists a factor set of the given extension of groups, which is bounded on one side.
So I get a counterpart to the necessary condition, which was found by Farkas in [3].DOI Code:
10.1285/i15900932v14n2p217
Full Text: PDF


