A new approach to constrained systems with a convex extension
Abstract
Systems S of N partial differential equations are considered, with M differential constraints and satisfying a convex supplementary conservation law. When M = 0, it is well known that these systems assume the symmetric hyperbolic form if the components of the mean field are taken as independent variables. To extend this property to the case 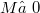 , a new system
, a new system 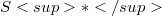 is here proposed with M supplementary variables
is here proposed with M supplementary variables 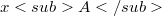 such that the solutions of
such that the solutions of 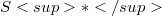 with
with 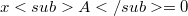 are those of the system S. Moreover S can be expressed in the symmetric hyperbolic form. This methodology is tested by applying it to the equations of the superfluid, modified from the classical Landau's formulation.
are those of the system S. Moreover S can be expressed in the symmetric hyperbolic form. This methodology is tested by applying it to the equations of the superfluid, modified from the classical Landau's formulation.
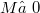 , a new system
, a new system 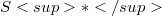 is here proposed with M supplementary variables
is here proposed with M supplementary variables 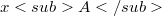 such that the solutions of
such that the solutions of 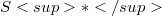 with
with 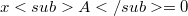 are those of the system S. Moreover S can be expressed in the symmetric hyperbolic form. This methodology is tested by applying it to the equations of the superfluid, modified from the classical Landau's formulation.
are those of the system S. Moreover S can be expressed in the symmetric hyperbolic form. This methodology is tested by applying it to the equations of the superfluid, modified from the classical Landau's formulation.DOI Code:
10.1285/i15900932v16n2p173
Full Text: PDF


